最佳逼近广义多项式(generalized polynomials of best approximation)是指达到最佳逼近的广义多项式,Haar提出了最佳逼近广义多项式的惟一性定理。
基本介绍最佳一致逼近问题在次数不超过n的多项式集合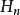 中求
中求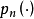 ,使它与
,使它与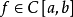 的误差
的误差
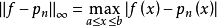
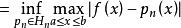 这就是最佳一致逼近问题1。
这就是最佳一致逼近问题1。
最佳一致逼近多项式给定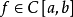 ,若存在
,若存在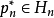 ,使
,使
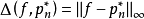
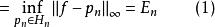 则称
则称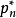 是
是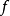 在[a,b]上的最佳一致逼近(minimaxapproximation)多项式,
在[a,b]上的最佳一致逼近(minimaxapproximation)多项式,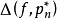 称为最佳偏差(minimax error),它等于最小偏差值
称为最佳偏差(minimax error),它等于最小偏差值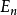 。
。
理论上已证明,对任何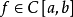 ,都存在惟一的
,都存在惟一的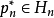 ,使式(1)成立,实际上在集合
,使式(1)成立,实际上在集合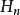 中每一元素,
中每一元素,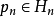 都对应一个偏差
都对应一个偏差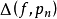 ,由于
,由于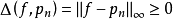 ,故集合
,故集合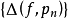 有下界,从而有下确界
有下界,从而有下确界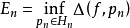 。如果存在
。如果存在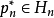 使
使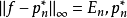 就是所要求的最佳一致逼近多项式。切比雪夫(Chebyshev)对最佳一致逼近多项式的特性,给出了下面的重要定理。
就是所要求的最佳一致逼近多项式。切比雪夫(Chebyshev)对最佳一致逼近多项式的特性,给出了下面的重要定理。
切比雪夫定理设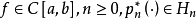 是
是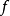 在[a,b]上的最佳一致逼近多项式的充分必要条件是,
在[a,b]上的最佳一致逼近多项式的充分必要条件是,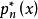 在[a,b]上至少有
在[a,b]上至少有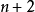 个点
个点
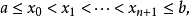 使
使
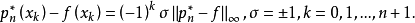
这个定理表明,最佳一致逼近多项式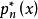 的特性,即
的特性,即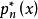 逼近
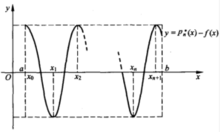
逼近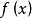 的误差分布是均匀的,如图1所示。
的误差分布是均匀的,如图1所示。
最佳(一致)逼近广义多项式若在空间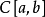 中取子集
中取子集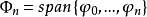 ,若存在
,若存在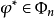 使
使
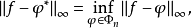 则称
则称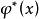 为
为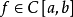 的最佳(一致)逼近广义多项式,对于代数多项式集合
的最佳(一致)逼近广义多项式,对于代数多项式集合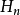 的元素
的元素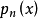 ,在[a,b]上最多只能有n个不同的零点,根据切比雪夫定理知最佳一致逼近多项式
,在[a,b]上最多只能有n个不同的零点,根据切比雪夫定理知最佳一致逼近多项式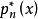 有n+2个轮流为“+”、“-”的偏差点,对广义多项式
有n+2个轮流为“+”、“-”的偏差点,对广义多项式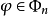 也要求在[a,b]上至多具有n个不同的零点,因此要对广义多项式引进更广泛的哈尔(Haar)条件1。
也要求在[a,b]上至多具有n个不同的零点,因此要对广义多项式引进更广泛的哈尔(Haar)条件1。
哈尔条件函数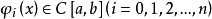 线性无关,若子集
线性无关,若子集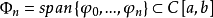 中任一不恒为零的广义多项式,即
中任一不恒为零的广义多项式,即
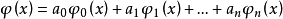 在区间[a,b]上至多具有n个不同的零点,则称函数
在区间[a,b]上至多具有n个不同的零点,则称函数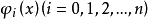 在[a,b]上满足哈尔条件,也可称子集
在[a,b]上满足哈尔条件,也可称子集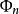 满足哈尔条件。
满足哈尔条件。
显然,子集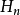 是满足哈尔条件的。
是满足哈尔条件的。
充要条件有了上述哈尔条件的定义,就可类似定理切比雪夫定理得到下面定理。
定理若子集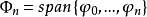 满足Haar条件则对任意给定的函数
满足Haar条件则对任意给定的函数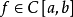 ,使广义多项式
,使广义多项式
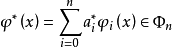 成为函数
成为函数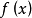 在空间C[a,b]上的最佳(一致)逼近广义多项式的充分必要条件是
在空间C[a,b]上的最佳(一致)逼近广义多项式的充分必要条件是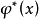 在[a,b]上至少存在n+2个轮流为“+”、“一”的偏差点,即
在[a,b]上至少存在n+2个轮流为“+”、“一”的偏差点,即
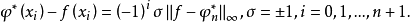 利用以上定理还可证明当子集
利用以上定理还可证明当子集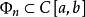 满足Haar条件时,则对任给的函数
满足Haar条件时,则对任给的函数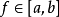 的最佳逼近广义多项式是惟一的。
的最佳逼近广义多项式是惟一的。
唯一性定理Haar还提出了下面的最佳逼近广义多项式的惟一性定理。
定理 对任何函数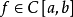 ,子集
,子集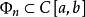 中存在惟一的最佳逼近广义多项式的充分必要条件是子集
中存在惟一的最佳逼近广义多项式的充分必要条件是子集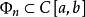 满足Haar条件1。
满足Haar条件1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

