预备知识邻域与有界集
设X是一个距离空间,A是X的一个子集,若存在x0∈X,及r>0,记
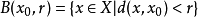
称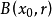 为
为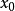 的一个r邻域,或简称邻域,使得
的一个r邻域,或简称邻域,使得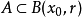 ,则称A为有界集。1
,则称A为有界集。1
内点与开集设M为距离空间X的子集,如果存在x的一个邻域整个包含于M,则称x∈M是M的一个内点。若M的所有点都是内点,则称M为开集。1
完全有界的设M是距离空间X中的一个子集,ε>0,N⊂M,若对任意x∈M,总存在y∈N,使得d(x,y)0,A总存在有限的ε-网,则称A是完全有界的。1
自列紧集距离空间中,闭的列紧集称为自列紧集。2
定义表述一列紧集(sequentially compact set)是度量空间中的一类子集。设A是度量空间X中的无穷集,如果A中的任一无穷子集必有一个收敛的点列,就称A是X中的列紧集。如果X本身是列紧集,就称X是列紧距离空间,简称为列紧空间。1
表述二设X是任一拓扑空间,又A⊂X,如果A的每个无穷子集都至少有一个聚点属于A,则A叫做拓扑空间X的一个列紧集。如果X作为空间X的点集是列紧的,则拓扑空间X叫做一个列紧空间。例如,任意空间的所有有限点集是列紧的;空集是列紧集I有限空间为列紧空间,列紧空间的每个闭集都是列紧集;每一个紧致空间都是列紧空间。3
性质有界集与列紧集(1)在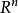 中,任意有界集是列紧集。1例如,根据包查诺-魏尔史特拉斯(Bolzano-Weierstrass)定理,数值线上任何有界集必是列紧的。4
中,任意有界集是列紧集。1例如,根据包查诺-魏尔史特拉斯(Bolzano-Weierstrass)定理,数值线上任何有界集必是列紧的。4
(2)在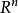 中,任意有界闭集是自列紧集。1
中,任意有界闭集是自列紧集。1
(3)列紧集的无穷子集是列紧集。2
列紧空间的子集(1)列紧空间内任意子集都是列紧集。
(2)列紧空间内任意闭列紧集都是自列紧集。
(3)列紧空间必是完备空间。1
必要条件和充要条件(1)距离空间X中集合是列紧的必要条件是M为完全有界的。
证明:设A为距离空间X的列紧集。如果A不是全有界的,则必存在某个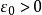 ,使得A没有有限的
,使得A没有有限的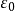 网。于是对于任意抽取的x1∈A,必存在x2∈A使得
网。于是对于任意抽取的x1∈A,必存在x2∈A使得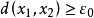 ,否则{x1}就是A的一个有限
,否则{x1}就是A的一个有限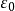 网。同理,存在x3∈A使得
网。同理,存在x3∈A使得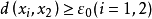 ,否则{x1,x2}就是A的一个有限
,否则{x1,x2}就是A的一个有限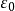 网,这样可以一直进行下去,于是我们得到一个点列{xn}使得当m≠n时,
网,这样可以一直进行下去,于是我们得到一个点列{xn}使得当m≠n时,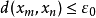 ,{xn}显然没有收敛的子列,与A的列紧性相矛盾,故A为完全有界的。5
,{xn}显然没有收敛的子列,与A的列紧性相矛盾,故A为完全有界的。5
(2)完备距离空间X中集合是列紧的充分必要条件是M为完全有界的。
证明:设A为完备的距离空间,A⊂X为全有界集.任取A中的一个点列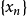 ,如果
,如果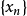 中只有有限个互不相同的元素,则
中只有有限个互不相同的元素,则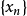 显然含有收敛的子列,因此,可设
显然含有收敛的子列,因此,可设 中有无限多个互不相同的元素,记这些元素构成的集合为
中有无限多个互不相同的元素,记这些元素构成的集合为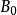 。
。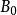 是全有界的,于是X中存在有限个以1/2为半径的开球使得这些开球的并包含
是全有界的,于是X中存在有限个以1/2为半径的开球使得这些开球的并包含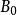 ,因此它们中至少有一个开球包含了
,因此它们中至少有一个开球包含了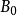 中无限多个元素,这些元素构成的集合记为
中无限多个元素,这些元素构成的集合记为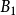 ,这个开球记为
,这个开球记为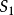 ,即
,即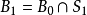 ,则
,则 ,且
,且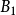 是无穷集。
是无穷集。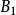 本身也是全有界的,将以上的论证应用于
本身也是全有界的,将以上的论证应用于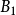 ,则存在
,则存在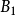 的子集
的子集 ,使得
,使得 中含有
中含有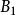 中无限多个元素且
中无限多个元素且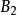 的直径不大于1/2。依此类推,我们可以找到一系列的集合
的直径不大于1/2。依此类推,我们可以找到一系列的集合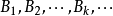 满足如下条件:
满足如下条件: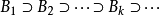 ,而且
,而且 的直径不大于
的直径不大于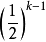 。每个
。每个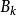 均含有
均含有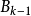 中无限多个元素。注意到每个
中无限多个元素。注意到每个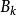 中的所有元素都是
中的所有元素都是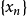 中的某些项,对于k=1,可取
中的某些项,对于k=1,可取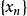 中的某一项
中的某一项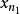 ,使得
,使得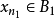 。对于k=2,可取
。对于k=2,可取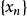 中的某一项
中的某一项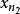 使得
使得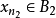 且可设
且可设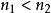 ,依此类推,便得到
,依此类推,便得到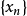 的一个子列
的一个子列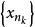 使得
使得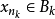 。根据
。根据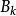 的性质,
的性质,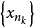 是基本点列,又因为X是完备的,故
是基本点列,又因为X是完备的,故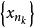 在X中收敛,于是A是列紧的。5
在X中收敛,于是A是列紧的。5
(3)设X是一个距离空间,M⊂X是紧集的充分必要条件为M是自列紧的。1
Arzelá-Ascoli定理X是列紧空间,F⊂C(X)是列紧的充要条件是F是一致有界并且等度连续的。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

