中心多项式是值域属于代数中心的特殊多项式,历史上第一个中心多项式是佛玛乃克(Formanek,E.)发现的。
定义设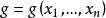 为自由代数
为自由代数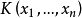 中的多项式,若
中的多项式,若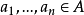 ,则称
,则称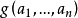 为
为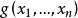 的赋值。所有赋值记为 g(A)。若 f 是代数 A 的恒等式,则对任意
的赋值。所有赋值记为 g(A)。若 f 是代数 A 的恒等式,则对任意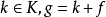 均有
均有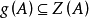 。任何使得
。任何使得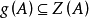 的其他多项式 g 都被称为 A 的一个中心多项式。
的其他多项式 g 都被称为 A 的一个中心多项式。
PI代数[PI-algebra]
若 K 代数 A 满足 K 上的 n 元自由代数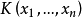 中一非零多项式
中一非零多项式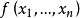 ,即
,即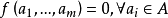 ,则称 A 是 K 上有多项式恒等式
,则称 A 是 K 上有多项式恒等式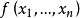 多代数,简称 PI 代数。并称
多代数,简称 PI 代数。并称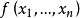 为代数 A 的恒等式 (identities of algebras)。交换代数为 PI代数,其满足多项式恒等式
为代数 A 的恒等式 (identities of algebras)。交换代数为 PI代数,其满足多项式恒等式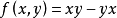 。
。
标准恒等式称恒等式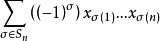 ,其中
,其中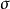 为偶置换时
为偶置换时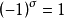 ,当
,当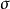 为奇置换时
为奇置换时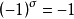 ,为 n 阶标准恒等式 (standard identities)。有限维代数为PI代数,事实上,域 K 上的 n 维代数满足 n+1 阶标准恒等式。
,为 n 阶标准恒等式 (standard identities)。有限维代数为PI代数,事实上,域 K 上的 n 维代数满足 n+1 阶标准恒等式。
卡普兰斯基定理(Kaplansky theorem):设 A 既是本原代数又满足 d 次多项式的PI代数 ,则 A 是其中心上的有限维单代数,其维数不大于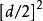 。这里
。这里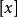 表示不大于 x 的整数。
表示不大于 x 的整数。
结合代数簇若 K 代数的集合 V 满足:① 如果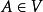 且
且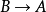 为单 K 代数同态,那么
为单 K 代数同态,那么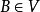 ;② 如果
;② 如果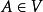 且
且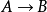 为满 K 代数同态,那么
为满 K 代数同态,那么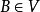 ;③ 如果
;③ 如果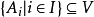 ,那么
,那么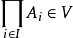 ,则称 V 为结合代数簇 (variety of associative algebras)。
,则称 V 为结合代数簇 (variety of associative algebras)。
设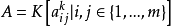 为以
为以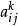 为未定元的交换多项式环,则由
为未定元的交换多项式环,则由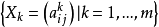 生成的
生成的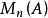 的 K 子代数称为 K 上的 n 次泛矩阵代数(generic matrix algebra)。1
的 K 子代数称为 K 上的 n 次泛矩阵代数(generic matrix algebra)。1
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

