黎曼流形

一黎曼度量的微分流形.设M是n维光滑流形，若在M上给定一个光滑的二阶协变张量场g，称(M，g)为一个n维黎曼流形，g称为该黎曼流形的基本张量或黎曼度量，如果满足：

1.g是对称的，即

g(X，Y)=g(Y，X) (X，Y∈TpM，p∈M).

2.g是正定的，即

g(X，X)≥0 (X∈TpM，p∈M)，

且等号仅在X=0时成立。

简单地说，黎曼流形就是给定了一个光滑的对称、正定的二阶张量场的光滑流形。

里奇曲率里奇曲率是截面曲率的一种平均。设(M，g)是黎曼流形，Ric(·，·)是其里奇张量，对任意的非零切向量X∈TpM，若：1

则称ρ(X)为黎曼流形M在切向量X所决定的方向上的里奇曲率。里奇曲率ρ(X)恰好等于包含X在内的各个二维切子空间上的截面曲率(参见“截面曲率”)的平均值.确切地说，若e1，e2，…，en-1∈TpM是与X正交的n-1个彼此正交的单位切向量，则：2

其中n=dimM。

曲率张量由联络确定的一个重要张量。设(M，)是仿射联络空间，R(X，Y)是曲率算子，其中X，Y∈Γ(TM).映射X，Y，Z→R(X，Y)Z给出了从Γ(TM)×Γ(TM)×Γ(TM)到Γ(TM)的C(M)线性映射，因此，它在每一点p∈M给出了从TpM×TpM×TpM到TpM的多线性映射，即它是一个(1，3)型张量场，称为(M，)上的曲率张量。在局部坐标系(U;x)下，记：

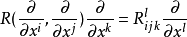
Rijk就是曲率张量的分量.由定义得到：

其中Γij是联络的系数。若(M，g)是黎曼流形，δ是其黎曼联络，则能够定义(M，g)上的4阶协变的曲率张量R(X，Y，Z，W)=g(R(X，Y)Z，W)。记：

(0，4)型曲率张量有下列性质：

1. R(X，Y，Z，W)=-R(Y，X，Z，W)

=-R(X，Y，W，Z).

2. R(X，Y，Z，W)=R(Z，W，X，Y).

3. R(X，Y，Z，W)+R(X，Z，W，Y)+R(X，W，Y，Z)=0.

数量曲率的概念数量曲率(scalar curvature)是里奇曲率的平均。设(M，g)是n维黎曼流形，R(·，·，·，·)是其曲率张量，对于TpM中的单位正交基{ei}，若：3

则S与单位正交基{ei}的选取无关，称S为M在点p的数量曲率.数量曲率S是在点p的各个切方向上的里奇曲率的平均值，即：

若用里奇张量在局部坐标系(U;x)下的分量来表示，则：

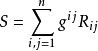
意义在黎曼几何中，数量曲率（或Ricci标量）是黎曼流形的最简单的曲率不变量。对于黎曼流形上的每个点，它分配由该点附近的歧管的固有几何确定的单个实数。具体来说，标量曲率表示在欧氏空间中，黎曼流形中的小测球的体积与标准球的体积的偏差量。在二维上，标量曲率是高斯曲率的两倍，并且完全表征了曲面的曲率。然而，在两个维度上，黎曼流形的曲率涉及多个功能独立的数量。

在广义相对论中，数量曲率是爱因斯坦 - 希尔伯特动作的拉格朗日密度。在量度变化下，拉格朗日的欧拉 - 拉格朗日方程组成真空爱因斯坦场方程，静态度量称为爱因斯坦度量。 n歧管的标量曲率被定义为Ricci张量的轨迹，并且其可以被定义为在某一点处的截面曲率的平均值的n（n-1）倍。

第一眼感觉，尺度至少为3的标量曲率似乎是一个微小的不变量，对歧管的全局几何形状几乎没有影响，但实际上一些深层定理显示了数量曲率的力量。一个这样的结果是Schoen，Yau和Witten的正质量定理。相关结果几乎完全了解哪些歧管具有正数量曲率的黎曼度量。4