简介

在数学中，特别是在差分拓扑中，莫尔斯理论使得人们可以通过研究该多面体的可微分函数来分析多面体的拓扑。 根据马斯顿·莫尔斯（Marston Morse）的见解，在多面体上的典型可微函数将直接反映拓扑结构。 莫尔斯理论允许人们找到CW结构并处理多面体的分解，并获得关于它们的同源性实质信息。1

在莫尔斯之前，亚瑟·凯利和詹姆斯·麦克斯韦尔（James Clerk Maxwell）在拓扑背景下开发了莫尔斯理论。 莫尔斯原来将他的理论应用于测地学（路径上能量函数的关键点）。 这些技术在Raoul Bott的周期定理的证明中被使用。

对复杂多面体而言，莫尔斯（Morse）理论的类比是皮卡德，莱夫谢茨理论。

基本概念为了说明这个概念，考虑一个山区景观M。如果f是函数M→R将每个点发送到其海拔高度，则R中的点的反像是山区景观的轮廓线。 轮廓线的每个连接分量是点形成的简单闭合曲线或具有双点的闭合曲线。 轮廓线也可以具有更高阶的点（三分点等），但是它们是不稳定的，这可以通过景观的轻微变形来去除。 轮廓线上的双点发生在鞍点处。 鞍点是周围景观在一个方向上向上弯曲并在另一个方向向下的点。2

想象一下，用水淹没这个景观。 然后，当水达到a的高度时，被水覆盖的区域是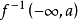 ，或者高度小于等于a的点。考虑这个区域的拓扑如何随着水的上升而变化，直观地看来，除了通过临界点的高度之外，它不会改变；也就是说，f的梯度为0的点（即雅可比矩阵作为从切线空间处的线性映射，那个地图f下的图像上的切线空间不具有最大等级），换句话说，这些水只能发生如下三点

（1）开始填满盆地；

（2）覆盖鞍座；

（3）淹没高峰。

对于这三个关键点中的每一种：流域、通道和峰值（也称为最小值，鞍形和最大值）。 直观地说，临界点b的指数是围绕b的独立方向的数量，其中f减小。 因此，盆地，山谷和山峰的指数分别为0,1和2。 严格来说，关键点的指数是在那一点计算的不确定矩阵的负定子子矩阵的维数。 在平滑地图的情况下，海森矩阵证明它是一个对称矩阵。

将Ma定义为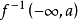 。离开拓扑的概念，当M是圆环定向并且f变化时，可以对M的拓扑如何变化进行类似的分析，其中f是投影一个垂直轴，指向它在平面上方的高度。

从圆环的底部开始，令p，q，r和s分别是索引0,1,1和2的四个关键点。 当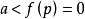 时，Ma为空集。 在通过p的等级之后，当 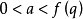时，Ma是与已经“附加到空集合”的点。 接下来，当 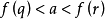时，Ma是圆柱体，并且与具有1单元格的同位素等价。 一旦a通过r的水平和 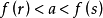，那么Ma是一个圆盘，其中一个磁盘被移除，这是一个相当于一个连接有1个单元的圆柱体的同伦。 最后，当a大于s的临界水平时，Ma是一个环面。

因此，似乎有以下规则：除了α通过临界点的高度之外，Mα的拓扑不变，并且当α通过指标γ的临界点的高度时，γ附加到Mα。 这不解决当两个关键点处于相同高度时会发生什么的问题。 这种情况可以通过轻微的扰动f来解决。 在景观（或嵌入欧几里德空间的多维数据集）的情况下，这种扰动可能只是稍微倾斜景观，或者旋转坐标系。

但是，这是错误的。 为了看到这一点，令M = R，令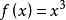 。 那么0是f的临界点，但当α通过0时，Mα的拓扑不会改变。实际上，索引的概念没有意义。 问题是二阶导数也为0，这种情况称为退化临界点。 请注意，这种情况是不稳定的：通过旋转图形下的坐标系，退化临界点被去除或分解成两个非退化临界点。

发展对于可微分多面体M上的实值平滑函数f：M→R，将f的不可微分点称为f的关键点，并将其在f下的图像称为临界值。 如果在临界点b，第二偏导数矩阵（Hessian矩阵）是非奇异的，则b被称为非退化临界点；如果海森是单数，那么b是一个退化的关键点。

对函数：

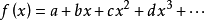
如果b = 0，则f在原点处具有临界点，如果c≠0（即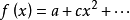 ），则为非退化，如果c = 0则为退化（即 ）。

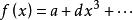f的非退化临界点b的指数是H的切线空间与M的最大子空间的尺寸，其中海森矩阵是负定的。 这对应于直观的概念，即索引是f减少的方向数。 关键点的简并性和指数与所使用的局部坐标系的选择无关，如西尔维斯特定律所示。

莫尔斯引理令b为f：M→R的非退化临界点。然后在b的邻域U中存在一个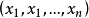 ，使得

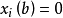
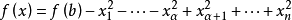
这里α等于在b点的f的指数。 作为莫尔斯引理的推论，人们看到非退化的关键点是孤立的。 （关于复杂域的扩展，请参阅复杂莫尔斯引理）。

基本定理多面体M上的平滑实值函数如果没有退化临界点，就是莫尔函数。 莫尔斯理论的一个基本结果表明，几乎所有的函数都是莫尔斯函数。 莫尔斯函数形成C2拓扑中所有平滑函数M→R的开放密集子集。 这有时表示为“一个典型的函数是莫尔斯”或“通用函数是莫尔斯”。

如前所述，我们对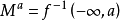 的拓扑何时变化的问题感兴趣，这个问题的一半是由以下定理给出的。

定理：假设f是M上的平滑实值函数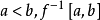， 是紧凑的，并且a和b之间没有临界值。 然后Ma与Mb不同，Mb变形缩回到Ma。了解当通过临界点时，Ma的拓扑如何变化也是有意义的。

这些结果推广并正式化了上一节所述的“规则”。 如上所述，所述的规则是不正确的；这些定理是正确的。

使用以前的两个结果和在任何可微分歧管上存在莫尔斯函数的事实，可以证明任何可微分歧管是指数n的每个临界点的n个单元的CW复合。 为了做到这一点，人们需要一个技术性的事实，人们可以安排在每个关键级别上有一个关键点，这通常通过使用梯度样的矢量场来重新排列关键点来证明。

封闭2维多面体分类应用莫尔斯理论已经被用来分类封闭2维多面体。 如果M是取向的，那么M被其属性g分类，并且与g句柄是不同的，所以如果g = 0，则M与2维多面体形成不同形状；并且如果g> 0，则M与g 2-tori的连接和形成不同形状。 如果N是无方向性的，则它被分类为数字g> 0，并且与真实投影空间RP2的连接和是不同的。 特别地，当且仅当它们是不同形态时，两个闭合的2维多面体是同胚的。

莫尔斯同源莫尔斯同源性是理解平滑多面体的同源性的一个特别简单的方法。 它使用莫尔斯函数和黎曼度量的通用选择进行定义。 基本定理是所得到的同源性是歧管的不变量（即独立于函数和度量）并且与多面体的奇异同源性是同构的；这意味着莫尔斯和单数贝蒂数字同意并给出了莫尔斯不平等现象的即时证明。 莫尔斯同源性的无限维度类似物被称为Floer同源性。

莫尔斯伯特理论莫尔斯函数的概念可以推广到考虑具有非多项关键点多项式的函数。 莫尔斯伯特函数是一个流形函数，其关键集是一个封闭的子集，其海森矩阵在正态方向上不退化。 （等效地，在关键点处的海森矩阵的核心等于关键子流形的切线空间）。莫尔斯函数是关键多面体为零维的特殊情况（因此临界点的海森矩阵在每个关键点都是非退化的 方向，即没有内核）。

该指数最自然地被认为是一对 。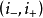

其中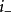 是临界歧管给定点处不稳定歧管的尺寸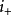， 是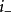 加上临界歧管的尺寸。如果莫尔斯伯特函数受到临界轨迹上的小函数的干扰，则扰动函数在非扰动函数的临界流形上的所有关键点的指数将位于i和i +之间。

莫尔斯伯特函数非常有用，因为通用莫尔斯函数很难使用;一个人能够可视化的功能，也可以容易地计算出来的功能通常具有对称性。他们往往会导致正面的关键歧管。拉尔·博特（Raoul Bott）在他原来的博特周期定理证明中使用了莫尔斯伯特理论。

圆函数是莫尔斯伯特函数的示例，其中关键集是（不相交的）圆。

莫氏同源性也可以用于莫尔斯博特功能；莫尔斯伯特同源性的差异通过光谱序列计算。弗雷德里克资产阶级在他的莫尔斯博特版本的辛普拉斯理论的工作过程中勾勒出一种方法，但由于实质的分析困难，这项工作从未出版过。3