简介

在数学中，卡尔松测度是对维度欧几里德空间Rn的子集的一种度量。 大致来说，域Ω上的Carleson测量是与Ω边界上的表面测量值相比，在Ω边界处不消失的度量。1

Carleson措施在谐波分析和偏微分方程理论中有许多应用，例如在Dirichlet问题与“粗糙”边界的解决方案中。 Carleson条件与泊松运算符的有界性密切相关。

Carleson测度以瑞典数学家Lennart Carleson命名。Carleson在20世纪60年代早期采用L. Carleson来描述开放单位盘中有界分析函数的代数中的内插序列，并给出了电晕问题的解决方案。

这些措施可以用以下方式定义：让我们对单位盘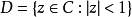做一个肯定的测量。 那么如果存在一个常数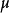，那就被称为Carleson度量，这样对于每个部分来说都是如此：

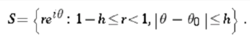
Carleson测度在复杂分析、谐波分析、BMO理论、积分运算符理论和等式理论中起着重要作用。

定义

令n∈N，令Ω⊂Rn为非空边界∂Ω的开放（即可测量）集合。 令μ为Ω上的Borel度量，令σ表示∂Ω上的表面度量。 如果存在常数C> 0，则测量μ被认为是Carleson度量，使得对于每个点p∈∂Ω并且每个半径r> 0，

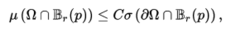
其中，

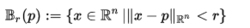
表示半径r的开放球约p。

泊松算子与卡尔松定理

令D表示配备有一些Borel测量μ的复平面C中的单位盘。 对于1≤p 0的集合的最小值：

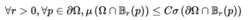
持有被称为测量μ的Carleson范数。

如果C（R）被定义为受限Carleson条件的所有常数C> 0的集合的最小值：

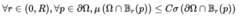
如果C（R）→0为R→0，那么测量μ被认为满足消失的Carleson条件。