庞特里亚金对偶性定理（Pontryagin dualitytheorem）是关于局部紧交换群与其对偶群的同构定理。

简介庞特里亚金对偶性定理是关于局部紧交换群与其对偶群的同构定理。

设G为局部紧交换群，Ĝ为G的对偶群。对x∈G，γ∈Ĝ记=γ(x)，则x可看做C上的特征标，从而有映射G→G:x→。庞特里亚金对偶性定理称：上述映射是拓扑群G到G上的同构。因此G等同于Ĝ，常记G=Ĝ。1

应用在数学上，特别是在调和分析与拓扑群的理论中，

庞特里雅金对偶定理解释了傅里叶变换的一般性质。它统合了实数线上或有限阿贝尔群上的一些结果，如：

实数线上够“好”的复数值周期函数能表成傅里叶级数，反之也能从傅里叶级数推出原函数。

实数线上够“好”的复数值函数有傅里叶变换；一如周期函数，在此也能从其傅里叶变换反推出原函数。

有限阿贝尔群上的复数值函数有离散傅里叶变换，这是在对偶群上的函数。此外，也从离散傅里叶变换反推原函数。

局部紧交换群(locally compact abelian group)

局部紧交换群是一类特殊的交换群。

设G是一个局部紧豪斯多夫空间，又是一个交换群，且映射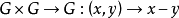是连续的，则称G为局部紧交换群，简称LCA群。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所