简介

非标准拓扑(nonstandard topology)是在非标准全域中展开的拓扑学。正像使用无限小数和无限大数可使微积分的基本概念更加直观，推理更加简明一样，在非标准全域中展开拓扑学，使用单子及饱和性可使拓扑学的基本概念更加直观，推理更加简明。

定义设(X，τ)是一个拓扑空间，其中X是任一非空集合，τ是X上的拓扑(τ是X的一些子集构成的族，空集和全集X属于τ，并且τ对有限交和任意并封闭)。设空间X及实数集合R都是标准全域*V(S)的个体集S的子集。并设相应的非标准全域V(S)是多饱和的，即基数不超过标准全域*V(S)的基数并且具有有限交性质的内集族的全交非空。更确切地说，若Aj∈V(S)，{Aj}j∈J具有有限交性质，并且J的基数≤card V(S)，则∩{Aj}j∈J≠∅。此时，X在*V(S)中的自然扩张*X是X的一个合适的非标准模型。设a∈X，则*X的子集：1

M(a)=∩{*O|a∈O并且O∈τ}

称为a的单子。若x∈M(a)，则称x近于a或近标准于a。.所有近标准点的集合记为：

ns(*X)={x∈*X|∃a∈X，x∈M(a)}.

用单子可以成功地描述“邻近”这个概念。由开集的定义可知，一个集合是开集当且仅当它的每一个点是它的内点(点a为集合A的内点，当且仅当A是a的一个邻域，即存在O∈τ，使得a∈O⊂A)，这反映了开集是包含它的每一个点的“邻近”所有点的集合。使用单子概念，可以更直观地说成：集合A是开集当且仅当*A中的每个标准点的单子包括*A中，即设A⊂X，A是开集当且仅当ᗄa∈A，M(a)⊂*A。事实上，若A是开集并且a∈A，则由单子的定义，M(a)⊂*A。反之，若A不是开集，则存在a∈A，a不是A的内点，即a的每个开邻域O与A的余集的交非空：O∩Ac≠∅。显然集族：

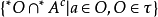
具有有限交性质。由多饱和性。

这个集合中的任一元素属于M(a)，但不属于*A。

再如函数的连续性，它的直观意义是把邻近的点映为邻近的点。标准的定义如下：设(X，T)，(Y，U)是两个拓扑空间，f：X→Y，f在点a连续，当且仅当对任意的U∈U(f(a))(f(a)的邻域系)，存在T∈T(a)(a的邻域系)，使得f(T)⊂U.这类似于用ε-δ来描述实连续函数。使用单子及饱和性可直接陈述为：f在点a连续，当且仅当：f(M(a))⊂M(f(a))，即把单子映到单子内。非标准方法在研究拓扑空间的紧性方面有更大的优点。可以证明，拓扑空间X是紧的当且仅当X的所有点是近标准点。这就把开集覆盖的性质转化为点集的性质.利用这个性质，很容易证明与紧性有关的定理，例如，吉洪诺夫定理——紧空间的乘积仍是紧空间。

非标准全域非标准全域是标准全域的非标准模型。它是另一个超结构的子集。设U=V(S)是一个以S为个体集的标准全域，I为指标集(I可取自然数集或更大的集合)，U为I上的一个自由超滤子，S是I到S的一切函数(I-序列)之集，即S={{ai}|ai∈S}，其中{ai}表示I到S的一个函数f：I→S，f(i)=ai(i∈I).在S上定义等价关系：{ai}～{bi}当且仅当{i∈I|ai=bi}∈U.这个等价关系简单地写成ai=bi，a.e..令S=S/～，以S为个体集的超结构记为V(S)。

标准全域U=V(S)的非标准全域U=V(S)是V(S)的一个子集，它的元素按如下方式归纳地选自V(S)。设{Ai}是V(S)中元素的一个I序列，若存在一个p∈N，使得Ai∈Vp(S)(i∈I)，则称序列{Ai}是有界的。若序列{Ai}是有界的，则存在一个最小的j∈N，使得{i|Ai∈Vj(S)}∈U，这个j称为序列{Ai}的秩。对于每个有界序列{Ai}，可以按秩归纳地选取一个元素A∈V(S)，并记A=〈Ai〉：若{Ai}的秩为0，令A=〈Ai〉，即S中的一个元素。假设对于秩小于j的每个序列{Bi}已经定义了对应的元素〈Bi〉，并且{Ai}的秩为j，则定义〈Ai〉={〈Bi〉|{Bi}的秩小于j，并且Bi∈Ai，a.e.}。这样就完成了非标准全域U=V(S)的定义。V(S)中的元素称为内的，V(S)\V(S)中的元素称为外的.由上述定义，S中的元素都是内的，因而没有外的个体。上述构造非标准全域的方法称为超幂构造。2

非标准全域也可用公理方法建立如下。设V(S)和V(S)分别是以S和S为个体集的两个超结构，嵌入映射：V(S)→V(S)满足如下两条公理：

扩张原理 S是S的真扩张，即S⫋S，并且对于每个a∈S，有a=a。

转换原理 标准全域的语言L(V(S))中的句子φ在V(S)中为真，当且仅当它的-转换φ在V(S)中为真。φ是把φ中出现的常元符号a全部换成它的-像的符号a得到的句子。.若A∈V(S)\S，则A称为标准集合，V(S)中的元素是内的，当且仅当它是某个标准集合的元素。所有内的元素构成的集合记为V(S)，它就是标准全域V(S)对应的非标准全域。

拓扑学现代数学的重要的分支学科。它研究几何形体在连续形变，精确地说，双方一一而且双方连续的变换(称为同胚)之下保持不变的性质。理解的广泛些，它是研究数学中连续性现象的学科。

拓扑学萌芽很早，但直到19世纪末才开始从不同的方面正式形成学科。20世纪末，拓扑学已发展为现代数学的一个庞大的学科，包括作为现代数学的基础的拓扑空间理论为核心内容的一般拓扑学，运用抽象代数的概念和方法为工具的代数拓扑学，进而派生出以流形为主要对象的微分拓扑学以及几何拓扑学等方面。拓扑学可简称为拓扑，但拓扑一词还可作为拓扑空间中的拓扑结构理解。

拓扑学最初被称为形势几何学(geometria situs)，这是莱布尼茨(Leibniz，G.W.)于1679年提出的，他预见到现在所称的组合拓扑学。最早为人所知的拓扑学定理可能是所谓的欧拉公式。欧拉(Euler，L.)于1750年发表了任何闭的凸多面体的顶点数v，棱数e和面数f有关系v-e+f=2。用现代说法，它是一个拓扑不变量，称为欧拉示性数。据史学家考证，笛卡儿(Descartes，R.)在1639年就知道它，并且莱布尼茨通过笛卡儿未发表的手稿于1675年得知这一结果。另一著名的结果是哥尼斯堡七桥问题的解决，欧拉在1736年将问题表成能否一笔画一个给定的图，并给出了一般性的解答.德国数学家高斯(Gauss，C.F.)于1827年得到曲面上曲率的积分与欧拉示性数的关系，他于1823年在电动力学中用线积分定义了空间中两条封闭曲线的环绕数。利斯廷(Listing，J.B.)于1848年第一次采用了拓扑学一词，其实他认为宁愿用形势几何，只是已被别人采作他用。黎曼(Riemann，B.)于1851年定义了黎曼面，引进了连通性和亏格，实际上解决了可定向闭曲面的分类问题，给拓扑学的建立以巨大的推动。1858年，默比乌斯(Mo¨bius，A.F.)和利斯廷独立地发现了单侧的曲面，现被更确切地称为不可定向曲面。默比乌斯于1863年恰当地指出形势几何学的定义。贝蒂(Betti，E.)于1870年定义了高维的连通性。若尔当(Jordan，C.)于1887年提出曲线定理，但证明是错的，直到1905年才得证。

拓扑学正式成为一门独立的学科是庞加莱(Poincaré，H.)实现的。他于1892年发表了题为“论形势分析”的短文，然后于1895年发表了题为“形势分析”的120页的长文，介绍它的概念，其中有同调、贝蒂数、相交、基本群，甚至隐含着上同调；建立了对偶定理和欧拉-庞加莱公式。随后直到1904年，他连续发表了五篇补充，为改进前述长文中的缺点创立了剖分方法，定义了挠系数，开始探讨三维流形的拓扑分类，构造出基本群不平凡而一维贝蒂数平凡的三维流形，并提出了著名的至今尚未解决的庞加莱猜想：基本群平凡的三维闭流形同胚于三维球面。这几篇文章奠定了组合拓扑学的基础，其思想之丰富，观念之深刻，影响之深远，一言难尽，但不够严密或缺乏证明，后来的进展正是从此入手，将这门学科建立在严格的逻辑上而发展为后来的组合拓扑学、代数拓扑学，进而发展出微分拓扑学等学科和分支。3