详细介绍

分式环的造法以及与它相关联的局部化方法大概是交换代数中最重要的技术性工具．它们相当于在代数几何图形里把注意力集中到一个开子集上或一点的近傍；这些概念的重要性是显然的2。

局部化，是分式环的另一名称，分式环(fractional ring)全称为“具有单位元的交换环R关于可乘子集S的分式环”．R的一个子集S若满足：(1)R的单位元e∈S,(2)S关于乘法是封闭的．则称S为可乘集．在集合

R×S={(r，s)|r∈R,s∈S}

中定义等价关系：(a,s)~(b,t)↔存在μ∈S,使(at—bs)μ=0．将(a，s)的等价类记为 ．在等价类所成集合中规定加法和乘法运算：

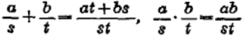
则该集合成环，称为分式环．记作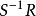 或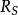 ．一般R不能嵌入 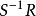中，但当S是R的所有非零因子集合时，R可以嵌入 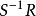中，这时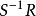 简称为R的分式环．若R还是整环。取S=R\{0}，则分式环 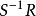就是R的商域．又如R为整数环Z，p为素数，取S=R\(p)，则分式环 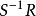是所有表成既约分式时分母与p互素的有理数全体所成的环3。

相关定理与性质定理14 交换环R可嵌人到它的分式环A中，R中非零因子在A中有逆元。若R有非零因子，则A是含单位元的环。

性质：

1)设p是A的素理想． 那么它的补集S=A\p是乘法封闭的(事实上A\p是乘法封闭的↔P是素理想)． 这时将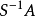 写作Ap．形如a/s的元素，这里a∈p，组成A中一个理想m．如果b/t∉ m，那么b∉p，因此b∈S，于是b/t是Ap中可逆元．由此推出，如a是Ap中的理想而a⊈m，那么a就含一个可逆元，因而是整个环．因此，m是环An中仅有的极大理想；换句话说，Ap是局部环．从A转化到Ap的过程叫做在p的局部化．

2)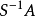 是零环↔0∈S． ．

3)设f∈A而S={fⁿ)n>0．这时将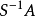写作Af．

4)设a是A中任一理想，并且令S=1+a是一切1+x，x∈a，所成的集．显然S是乘法封闭的2．

更多内容请参考书籍《现代数学译丛 交换代数导引》等。