算术化（哥德尔编码）

哥德尔使用基于素数因数分解的哥德尔编码系统。他首先把唯一的自然数指派到在他所处理的算术的形式语言中的每个基本符号。

为了编码是符号序列的整个公式，哥德尔使用了如下系统。给出正整数的序列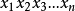，哥德尔对这个序列的编码是第n个素数自乘这个序列中对应值的次数：

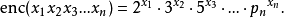
依据算术基本定理，用这种方式获得的任何数都可以唯一的因数分解到素因子，所以可以有效的从其哥德尔数恢复最初的序列。

哥德尔特别的在两个级别使用这个方案：首先编码表示公式的序列，其次编码表示证明的序列。这允许他证明在关于自然数的命题和关于自然数的定理的可证明性的命题之间的对应，这个证明的关键观察。

有更复杂的(但更“简洁”)的方式来构造序列的哥德尔数1。

唯一性的缺乏哥德尔编号不是唯一的。一般性的想法是把公式映射自然数上。假设有K个基本符号。可替代的哥德尔编码可以通过把每个基本符号映射到基数为K的记数系统的一个数字来构造，这样由n个符号的字母串构成的公式 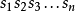将被映射成数

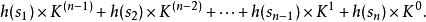
换句话说，借由将K个基本符号以某种固定顺序摆放，那么每个方程式就会产生唯一对应的哥德尔数。但是如果将K个基本符号以另一种固定顺序摆放，则会产生另一种哥德尔编号2。

形式系统应用还有，哥德尔编号蕴涵了形式系统的每个推论规则都可以被表达为自然数的函数。如果f是哥德尔映射并且如果公式C可以推导自公式A和B，通过推论规则r，就是说

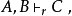则有某个自然数的算术函数gr使得

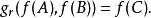
接着，因为这个形式系统是形式算术的，它能做关于数和它们相互的算术联系的陈述，可以得出这个系统也可以通过哥德尔编号的方式，间接的做关于自身的陈述：就是说，形式系统的一个命题可以做出断言，在从哥德尔映射的角度查看的时候，能转换成关于同一个形式系统的其他命题，甚至是自身的断言。所以，通过这种方式一个形式算术可以做关于自身的断言，而成为自引用的，就像二阶逻辑。这提供给哥德尔(和其他逻辑学家)一种探索和发现关于形式系统的一致性和完备性性质的一种方法3。