在数学，特别是点集拓扑学中，拓扑空间的子集S的完备集是S的所有极限点的集合。

简介在数学，特别是点集拓扑学中，拓扑空间的子集S的完备集是S的所有极限点的集合。它通常记为S'。1

这个概念是格奥尔格·康托尔在1872年介入的，他开发集合论很大程度上就是为了研究在实直线上的导出集合。

完备集公理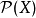 完备集是拓扑学的基础概念之一，可以用来定义拓扑空间。 给定集合X，考虑一个定义在X的幂集上的运算 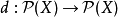，若d满足以下完备集公理，则称d为完备集运算：

D1：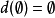

D2：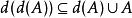

D3：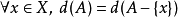

D4：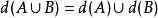

d(A)称为A的完备集。

相关概念聚点

d(A)中的点称为A的聚点。

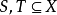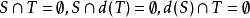性质，若。则称S和T是分离的。（注意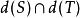：不一定为）。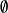

集合S被定义为完美的，如果S=d(S)。等价地说，完美集合是没有孤点的闭集。完美集合又称为完备集合。

Cantor-Bendixson定理声称任何波兰空间都可以写为可数集合和完美集合的的并集。因为任何波兰空间的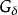子集都再次是波兰空间，这个定理还证明了任何波兰空间的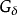子集都是可数集合和完美集合的并集。

拓扑空间X是T1空间，当且仅当。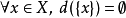

参见极限点

导出代数

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所