概念
降维法是把一个多因素问题转化成一个较少因素(降低问题的维数)问题,而且较容易进行合理安排,找到最优点或近似最优点,以期达到满意的试验结果的方法。主要类型有纵横对折法、等高线法和平行线法。2
分类与介绍依安排试验步骤的差异,降维法可分为纵横对折法、等高线法和平行线法。下面主要介绍一下常用的等高线法。3
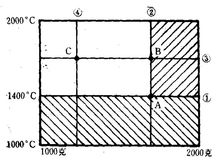
等高线法第一步是根据经验,把一个因素固定在适当的位置上。如无经验可凭,可先把一个因素固定在它的选值范围的0.618处。然后对第二个因素进行优选。第二个因素选到较好的点就将第二个因素暂时固定,对第一个因素进行优选。这样交替进行最优逼近,直到取得满意的结果为止。
以熔炼特种钢,对温度因素和特殊元素加入量因素进行优选为例,说明等高线法的应用。 已知温度的范围是1000—2000℃;某元素的加入量是1000—2000克。见图1 依经验先把温度固定在1400℃。在直线①上对元素加入量进行单因素优选,得到最好点A;再在过A点的直线②上对温度进行优选得到②上的最好点B;沿着A所在直线①舍去不含B点的范围,再通过B点做直线③,在③上对加入量进行优选,找到③上的最好点C;再沿着B所在直线②舍去不含C点的范围。如此继续下去,在过C点的直线④上选择最佳温度……,直到取得满意结果为止。
等高线法是双因素降维法较常用的一种适用性较普遍的一种方法。 3
纵横对折法纵横对折法是与等高线法相似,但每次取值都在取值范围的1/2处(类似对分法)的一种双因素降维法。 3
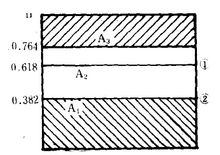
平行线法平行线法是适用于两因素中有一因素不易调变的情况。按单因素的0.618法在不易调变的因素上取值,并将其固定,再对另一因素按单因素优选法优选,得到最优值后,比较取舍。见图23
流程降维法的流程如下:
(1)把立体图形转化为平面图形1
把立体图形转化为平面图形需要稍许空间想象力,可参考图形推理中的折纸盒问题提升相应的能力。行测考试中,需要转化为平面图形的立体图形一般比较规则,多是立方体或四面体。
(2)把问题对应在平面图形下就是把原问题对应在转化后的平面图形下。
示例:求立体图形两点间沿外表面的最短路径,在把立体图形展开为平面图后,就是求平面上对应点间的最短路径。
(3)用平面几何知识求解
即对化简后的平面问题用平面几何知识分析求解。1
适用范围在考试中,降维法主要应用于立体图形的几何问题,利用这个方法,把立体图形转化为平面图形,降低题目难度。1
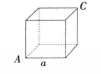
例题分析一只蚂蚁从3图的正方体A顶点沿正方体的表面爬到正方体C顶点。设正方体边长为a,问该蚂蚁爬过的最短路程为多少?1
解析:
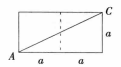
把表面展开,将A与C置于同一平面中,如图4所示只有一种展开方式。
原问题中涉及两个顶点A、C,那么展开后原问题简化为求平面图上A、C两点之间的最短路径。
在同一平面上,两点之间的线段最短,因此计算AC的长度:
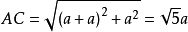
即最短路径为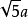 。
。


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

