定义
图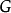 的正常着色(简称着色)一般是指对它的每一个结点指定一种颜色,使得没有两个邻接的结点有同一种颜色。如果图
的正常着色(简称着色)一般是指对它的每一个结点指定一种颜色,使得没有两个邻接的结点有同一种颜色。如果图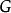 着色时用了
着色时用了 种颜色,则称图
种颜色,则称图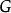 为
为 -可着色的,对于图
-可着色的,对于图 着色时,需要的最少颜色数称为着色数,记作
着色时,需要的最少颜色数称为着色数,记作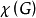 。2
。2
相关性质定理定理1 任意平面图最多是5-可着色的。
定理2 (四色定理)任何平面图都是4一可着色的。2
定理3 若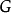 是简单图,则
是简单图,则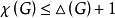 。3
。3
证明: 对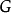 的阶数n进行归纳。
的阶数n进行归纳。
当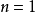 时,
时,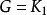 ,这时△=0,
,这时△=0,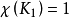 ,结论成立。
,结论成立。
设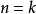 时结论成立。考虑
时结论成立。考虑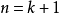 时的情形,任取G中一个结点
时的情形,任取G中一个结点 。令
。令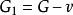 ,则
,则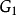 是k阶简单图,由归纳假设
是k阶简单图,由归纳假设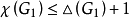 ,另一方面
,另一方面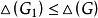 ,于是有
,于是有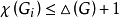 ;设在G中
;设在G中 的邻接点是
的邻接点是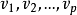 ,则
,则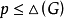 ,因此,用
,因此,用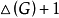 种颜色对
种颜色对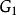 正常点着色时,
正常点着色时,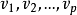 最多只能用其中的
最多只能用其中的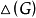 种颜色,即至少可以剩下一种颜色用于
种颜色,即至少可以剩下一种颜色用于 的着色,这就是说
的着色,这就是说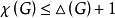 。
。
当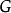 是完全图和奇圈时,定理中等号成立,Brooks进一步证明过,对于既不是完全图也不是奇圈图的简单连通图
是完全图和奇圈时,定理中等号成立,Brooks进一步证明过,对于既不是完全图也不是奇圈图的简单连通图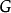 ,不等号严格成立,即在这种情况下有
,不等号严格成立,即在这种情况下有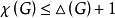 。
。
决定一个图的色数不是一件容易做的工作,事实上人们还未找到一个普遍有效的方法,但是也有一些很好的近似方法可以利用。3
着色方法韦尔奇·鲍威尔法用韦尔奇**·**鲍威尔法可以用最少的颜色数对任意图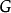 进行正常着色,该方法的步骤如下:
进行正常着色,该方法的步骤如下:
(1)将图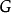 中的顶点按度数递减的次序进行排列(如果有相同度数的顶点,这种排列是不唯一的);
中的顶点按度数递减的次序进行排列(如果有相同度数的顶点,这种排列是不唯一的);
(2)用一种与已着色顶点所有颜色不同的新的颜色C对排列最靠前的尚未着色的顶点着色,并按排列次序对与前面已着上颜色C的顶点不邻接的每一顶点着同样的颜色C;
(3)反复重复步骤(2),直到所有顶点全部着上颜色为止;
整个过程所用的颜色数即为该图的色数。3
独立集分划法定理 令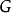 是色数为
是色数为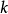 的图,则存在下述着色方式:
的图,则存在下述着色方式:
(1)着第一种颜色的结点构成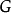 的一个极大独立集
的一个极大独立集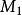 ;
;
(2)对每个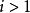 ,着第
,着第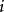 种颜色的结点构成
种颜色的结点构成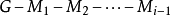 的极大独立集
的极大独立集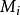 。
。
根据这个定理。可以构造如下方法:
第一步:求出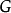 中全部的极大独立集;
中全部的极大独立集;
第二步:对前面已求得的每个极大独立集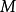 ,构造图
,构造图 ;
;
第三步:对第二步中构造的图找出全部的极大独立集.冉类似地重复第二步。
显然,当某一步得到的子图是个零图时,这个零图的结点构成图的一个独立集,从原图得到这个零图的过程中每次删去的极大独立集全体构成了结点集的一个独立分划。
上述方法就是找出所有的这种分划,其中由分块数最少的分划给出图的色数。但是,这种方法的工作量太大,经过改进,人们证明只需在上述方法中把求全部极大独立集改为求包含图的最大度结点的全部极大独立集就行了,尽管如此,求色数的工作量仍是相当可观的。3
举例分析例1 求图1所示的图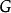 的色数。
的色数。
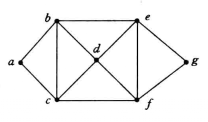
**解:用韦尔奇·**鲍威尔法对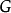 进行着色,整个过程如表1(a)~(d)所示。
进行着色,整个过程如表1(a)~(d)所示。
|| || 表1
将图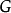 中顶点按照度数由大到小排序,得到序列
中顶点按照度数由大到小排序,得到序列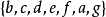 ,首先,将顶点b着上红色,并且将与b不邻接的顶点
,首先,将顶点b着上红色,并且将与b不邻接的顶点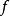 也着上红色;其次,将顶点c着上黄色,并将与c不邻接的e也着上黄色;接下来,将顶点d着上蓝色,并将与d不邻接的a也着上蓝色,g与d和a均不邻接,因此它也可以着上蓝色,这样整个着色过程就结束了,
也着上红色;其次,将顶点c着上黄色,并将与c不邻接的e也着上黄色;接下来,将顶点d着上蓝色,并将与d不邻接的a也着上蓝色,g与d和a均不邻接,因此它也可以着上蓝色,这样整个着色过程就结束了,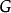 的色数
的色数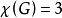 。
。
例2 考试安排问题,期末每个学校都要举行考试,设学校开设的课程集合为X,学生集合为Y,要求学同一门课程的学生考试时间尽可能相同,问至少要举行多少场考试?
对于这个问题,可以用一个图G来描述,结点表示考试课目,结点 和
和 邻接当仅当有学生既要参加
邻接当仅当有学生既要参加 课程的考试,又要参加
课程的考试,又要参加 课程的考试,那么,所得图的每一种点着色方案都给出了考试的一种安排方式。而最少的考试场次正好对应着找图的点色数。3
课程的考试,那么,所得图的每一种点着色方案都给出了考试的一种安排方式。而最少的考试场次正好对应着找图的点色数。3


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

