定义

如果一个图能够画在平面上，使得顶点集合及边集合分别是相同的，而如果边相交仅在边的端点处，则称这个图是可嵌人平面的，或称作可平面图(planar graph)；否则称作不可平面图，可平面图G的这样一种画法称为G 的一个平面嵌入(planar embedding)。

如果一个可平面图重新画在平面上，使得没有两条边相交，除非在顶点处，则称这个图是平面图(plane graph)1。

相关性质定理平面图的度定理设G是平面图，记m是G的边数，则

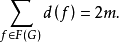
**证明:**图中的一条割边是关联一个面的，对该面的度贡献为2；一条非割边是关联两个不同的面的，并分别对这两个面的度贡献为1，因此，将所有面的度求和时，每条边用了两次。

平面图的欧拉公式及其应用不难发现，在连通平面图中有一个关于顶点、边及面的数目的简单公式，因为欧拉(Euler)首先对多面体的顶点和边所定义的平面图建立了这个公式，所以该公式以欧拉命名。

平面图的欧拉公式： 设G是无向连通平面图，具有n 个顶点，m条边和r个面，则 n-m+r=2。

推论1如果G是平面图，则n-m+r=w+1，其中，w是G的连通分支数。

推论2 一个连通可平面图的所有平面嵌人都有相同的面数。

**证明：**这是因为一个连通可平面图的所有平面嵌人都是彼此同构的，因此在顶点数、边数都分别相同的情况下，利用平面图的欧拉公式，直接证得。

推论3如果G是顶点数大于等于3的简单可平面图，则m≤3n－6。

推论4 K5是不可平面图。

**证明：**因为K5是顶点数为5的简单图，其m=10，n=5，3n－6 =9，有m>3n- 6，由推论3，得证K5是不可平面图。

推论5K3,3是不可平面图。

**证明：**利用K3,3是一个简单的二部图，其任一个回路的长度至少是4，如果它是可平面图，其边数应小于等于2n-4，但是，K3,3的n=6，m=9，2n-4=8，m>2n-4，所以K3,3是不可平面图。

推论6

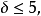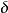如果G是简单的可平面图，则其中表示图G的最小度1。

可平面图的判定虽然欧拉公式可用来判别某个图是不可平面图，但是当顶点数和边数较多时，应用欧拉公式进行判别就会相当困难。一个图是否有平面的图形表示是判别可平面图的最具说服力的方法，但是又因为工作量太大而不实用，要找到一个好的方法来判断任意一个图是否是可平面图，就得对平面图的本质有所了解，已经分别证明了K5和K3,3是不可平面图，而它们的任何真子图却是可平面图，波兰数学家库拉托夫斯基(Kuratowski，1930)给出了平面图的一个异常简单的特性1。

细分设G是一个无自环边的无向图，去掉它的一条边{u，v}，并且用两条新的边{u,w}和{w,v}替换它，其中，顶点w不是图G 的顶点，通过添加每个度为2的一个或多个新的顶点，按照这样的方法得到的新图，称作G 的细分(subdivision)。

显然，如果一个图G是可平面图，那么G的每个细分也是可平面图；并且如果图G是不可平面图，则G的每个细分也是不可平面图。

库拉托夫斯基Kuratowski定理一个图G是不可平面图的充分必要条件是G 包含K5或K3,3，或者K5或K3,3的细分作为它的子图。

由于该定理的证明比较复杂，所以在此省略1。