基本概念李亚普诺夫稳定性

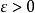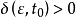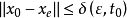在1892年，俄国数学家李亚普诺夫（Lyapunov）提出将判定系统稳定性的问题归纳为两种方法：李亚普诺夫第一法和李亚普诺夫第二发 ，都对应存在另一实数 ，使当 时，从任意初始状态x0出发的解都满足：

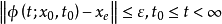则称平衡状态 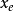为李亚普诺夫意义下稳定。1

李亚普诺夫第二法李亚普诺夫第一法又称间接法，是利用系统状态方程的解来判定稳定性，需要引入线性近似并求解方程。

相比之下，李亚普诺夫第二法（又称直接法）直接从系统运动方程出发，通过构造李亚普诺夫函数，并分析它和它的一次导数的符号特性来获得系统稳定性的有关信息。2

李亚普诺夫方程就是从直接法中推导而来的一个线性定常系统稳定性判据方程。

李亚普诺夫方程形式为，

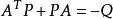这个方程作为稳定判据表示的是，对于没有外部输入的线性定常连续系统，其原点平衡状态渐进稳定的充分必要条件为：对于任意给定的正定对称矩阵Q，有唯一的正定对称矩阵P使李亚普诺夫矩阵方程成立2。

判定和使用方法稳定性判定使用李亚普诺夫第二法的条件是构造李亚普诺夫函数V(x)，该函数是定义的一个正定标量函数，作为虚构的广义能量函数。

对于一个给定系统，若能找到V(x)是正定的，而其一阶导数是负定的，则这个系统是渐进稳定（渐进稳定是指在李亚普诺夫稳定的前提下，时间趋于无穷时，系统能够达到稳定状态）的。

对于线性定常系统，可以利用李第二法相关定理导出简化判据，即李亚普诺夫方程判据。

构造函数如果得到了李亚普诺夫方程，

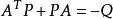
则李亚普诺夫函数可以构造为：

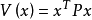
也就可以通过李函数对系统的稳定性进行分析。

Matlab求解在Matlab软件中，使用X=lyap(A,C)可以求解满足李雅普诺夫方程的对称矩阵X；离散系统可用X=dlyap(A,C)求解对称矩阵X。