概述

根据状态分类的定义，所有状态分为非常返态和常返态两类。

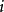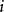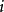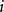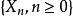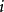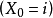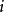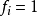非常返状态亦称瞬时状态，换句话说，马尔可夫链的状态 称为非常返的，如果链从状态 出发，它将以正的概率不再返回 。常返状态亦称必回状态，是马氏链将无限次地返回的状态。设 是齐次马尔柯夫链 的一个状态。如果链自 出发即 ，最终将命中 的概率 ，则称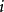为链的必回状态。对必回状态 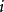，链自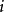 出发必然无限次的返回 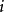，故而称为常返状态。

简单的说，对于任一状态 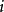，设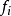 为过程从状态 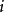出发，在未来某一时刻再次返回状态 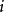的概率。如果 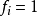，那么称状态 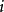是常返的，如果 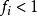，那么称状态 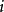是非常返的。2

非常返状态又进一步分为正常返状态和零常返状态，其中正常返状态包括周期状态和非周期状态。遍历状态指的是非周期的正常返状态。注意这里的遍历性指过程无指定间歇地、频繁地返回，是一个状态的性质，这与平稳过程的遍历性是不同的。1

遍历性在电力运行、机械加工、大规模的劳动组织等生产过程中，常常会遇到这样的情况，情况，即不管系统的初始状态如何，在经历了一段时问以后，系统就会处于统计平衡状态(Statistical Equilibrium)。这种情况就是数学中所谓的遍历性问题，遍历性问题是马氏链理论的一个重要部分。

现给出遍历性问题的严格数学定义：

设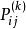为齐次马氏链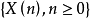的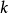 步转移概率，如果对一切 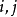，存在不依赖于 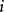的极限

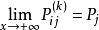
则称马氏链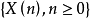具有遍历性。若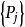构成一个概率分布，则称该马氏链存在着极限分布。

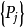通过上文还得出了两个不加证明的遍历定理，它们解决了在怎样的条件下齐次马氏链具有遍历性以及求极限分布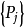 的方法。3

遍历定理（1）对于有限状态齐次马氏链，如果存在正整数 ，并且对所有的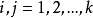 都有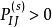 成立，则该马氏链必具有遍历性，且 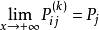中的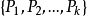即为极限分布，它是方程组 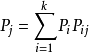满足条件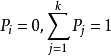 的唯一解。

（2）不可约非周期的可列状态齐次马氏链存在平稳分布的充要条件是，这个链的所有状态都是正常返的，且这时极限分布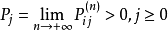是唯一的平稳分布。3

周期状态和非周期状态称正整数集合 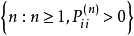的最大公约数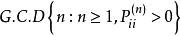为状态 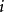的周期，记之为 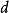。或者说，状态 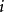是具有周期 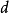的周期性状态。特别地，当 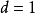时，则称状态 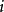是无周期的。当 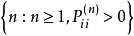为空集时，不考虑 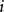的周期。

例如，过程从状态 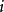出发，若只有当 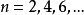时，过程才有可能返回状态 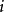，那么取 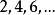的最大公约数 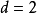，则 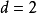是过程的周期。这时，我们说过程是周期性的，或说状态 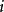是周期性状态。

若 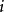是周期为 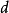的周期性状态，则仅当 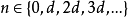时，才存在 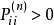，或者说，除了 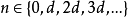以外，则均有 。

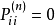如果除了 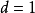以外，各 值中没有其他公约数能使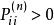 ，则称状态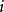 是非周期的。

非周期的正常返态称为遍历状态。