概念

细拓扑(fine topology)是由给定的下半连续函数族确定的、比原来拓扑细的一种拓扑。在非空集合Ω上赋予拓扑T，设Φ是一族从(Ω，T)到[0，+∞]的下半连续函数组成的凸锥(设+∞∈Φ)，把形如：

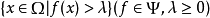
的集全体记为S，那么S∪T所生成的拓扑T0是使Φ中每个函数都连续的最粗拓扑，称之为(相对于Φ与T的)细拓扑。细拓扑下的开集、闭集、闭包、极限等分别称为细开集、细闭集、细闭包、细极限等。在格林空间中，若不另作申明，则总认定Φ是非负超调和函数全体。一般地，谈及细与瘦的概念时，都假定有了确定的Φ与T。

拓扑拓扑是集合上的一种结构。设T为非空集X的子集族。若T满足以下条件：

1.X与空集都属于T;

2.T中任意两个成员的交属于T;

3.T中任意多个成员的并属于T;

则T称为X上的一个拓扑。具有拓扑T的集合X称为拓扑空间，记为(X，T)。

设T1与T2为集合X上的两个拓扑。若有关系T1T2，则称T1粗于T2，或T2细于T1。当X上的两个拓扑相互之间没有包含关系时，则称它们是不可比较的。在集合X上，离散拓扑是最细的拓扑，平凡拓扑是最粗的拓扑。

下半连续函数下半连续函数是指其上方图形为闭集的函数。设X是拓扑空间，f：X→R∪{+∞}，f≢+∞.若在x0∈X有网：

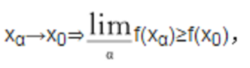
则称f在x0为下半连续。若f在X中每点均为下半连续，则称f在X上为下半连续。.f：X→R∪{+∞}为下半连续⇔ᗄc∈R，fc={x∈X|f(x)≤c}是X中的闭集⇔epi(f)={(x，t)∈X×R|f(x)≤t}是X×R中的闭集。若在上述定义中，将网xα换为序列xn，则得到f为依序列下半连续的概念。当然，在度量空间中，此二概念等价。当函数(-f)：X→R∪{+∞}为下半连续时，则称函数f：X→R∪{-∞}为上半连续。f在某点为连续，等价于f在此点既上半连续又下半连续。紧拓扑空间上的下半连续函数或序列紧拓扑空间上的依序列下半连续函数可达到其下确界。2

凸锥凸锥是一类特殊的凸集。实线性空间中既是凸集又是锥的集合称为凸锥。凸锥C满足C+C⊂C。对于X中的任何子集A，由它生成的凸锥是其元素的所有正线性组合的全体。而当A是凸集时，由A生成的凸锥就是λA。如果凸锥C满足C∩(-C)={0}，那么经常用它来定义实线性空间中的半序关系。对于x，y∈X， 定义x≥y为y∈x+C。则≥满足：

1.x≥x.

2.x≥y，y≥x⇒x=y.

3.x≥y，y≥z⇒x≥z.

子概念开集开集是拓扑空间的基本概念之一。在集合X上确定适当的拓扑结构T后，T中的元素就称为T开集，在不致混淆时亦简称开集。拓扑T亦称为开集系。开集的补集是闭集，开集G的每一点都是G的内点，G也是G的任一点的邻域。开集、闭集、内部、闭包等概念都是康托尔(Cantor，G.(F.P.))在研究欧几里得空间的子集类时引进的。豪斯多夫(Hausdorff，F.)于1914年将它们推广到抽象空间。

闭集闭集是拓扑空间的基本概念之一。拓扑空间中开集的补集称为闭集。集合A是闭集当且仅当A等于它的闭包，或A的每个聚点都属于A。拓扑空间X中闭集的全体称为X的闭集系。由闭集的定义可得到与开集对偶的三条性质：

1.空集∅与X均为闭集。

2.任意多个闭集的交是闭集。

3.任意两个闭集的并是闭集。

闭包闭包是图论的一个基本概念。指由一个图所派生出的另一个图。具体地说，一个图G的闭包H是指符合下列条件包含边最少的图：G是H的支撑子图；对于H上任何两不相邻节点v和w，都有ρH(v)+ρH(w)