正式定义域名是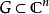 使得功能

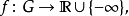
有多个分谐波方式是一个（多次调和），它上半一个，所有复杂的线性

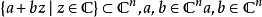
功能反对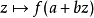 说下一组是次谐波的：

具有完整的一般性，这个概念是一个任意复杂的流形和复杂的分析空间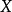 但可以定义如下。一些上半连续功能

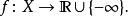
多次调和条件是一个任意的正则映射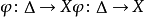 功能反对

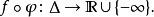
有劣和谐，不能不说是。这里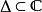 代表一个单位磁盘。

可微分多重劣调和函数

有类（可能有区别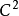） 当属于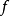 是一个多通道谐波，其必要和充分的条件是组件

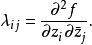
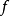它是一个半确定的Hermitian矩阵，被称为Levy矩阵。虽然它是相同的价值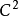， 函数f是多次谐波的充分必要条件如下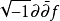： 1。

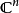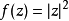示例与Kohler流形的关系：n维复数欧几里德空间 以上 是一个多重调和函数。其实 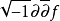，除了时间不变 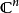相当于上面的标准科勒格式。更一般地说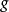， 有一定的科勒格式 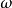另一方面，

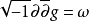
满意了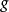， 是一个多重分谐波函数，被称为科勒势能。

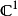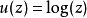与狄拉克三角洲的关系：1维复数欧几里得空间 以上， 是一个多重调和函数。 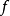是一个具有紧凑平台的类函数，从柯西积分公式，

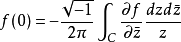
它可以转换成以下形式。

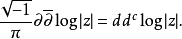
这是从0开始的狄拉克测量，这不是别的。

历史1942年，Okazaki和Pierre Ruong（英文版）定义了多个次谐波函数（多次调和函数2）。

性质多个次谐波函数（多次调和函数）集在半连续函数向量空间中形成凸锥。即，以下成立。

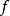是一个多重调和函数 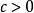如果它是一个正实数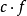， 也是多谐波。

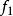和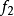 是一个多重分谐波函数，然后求和 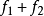也是多谐波。

多重谐度是一个本地属性。也就是说，该函数是多次谐波的，相当于在每个点附近是多串谐波。

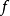是多从属的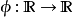， 是一个单调递增的凸函数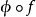， 是多从属的谐波。

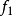和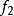 如果它是一个多重谐波函数，一个函数 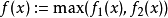也是多从属的。

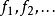是一个单调递减的多重谐波函数系列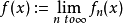， 也是一个单调递减的多次谐波函数。

所有连续的多次谐波函数可以作为单调递减的一系列平滑多次谐波函数的极限得到。此外，这一行可以被选为统一收敛序列。

正态半连续的不等式条件保持为方程。也就是说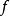， 是多排谐波，以下为成立。

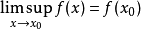
多重次调和函数是可选的科勒称重对分谐波方式是。

因此，多个谐波函数满足最大值原则。也就是说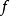， 有巩固开放区域 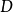上面是多次谐波，D中的 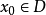针对

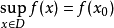
如果它成立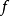， 是一个常数3。