由来

天文学家哈密顿(William Rowan Hamilton) 提出，在一个有多个城市的地图网络中，寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径。

这个问题和著名的七桥问题的不同之处在于，过桥只需要确定起点，而不用确定终点。哈密顿问题寻找一条从给定的起点到给定的终点沿 途恰好经过所有其他城市一次的路径。1

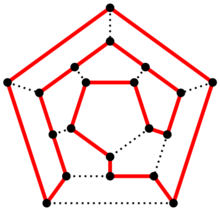
汉密尔顿回路哈密顿路径问题在上世纪七十年代初，终于被证明是“NP完备”的。据说具有这样性质的问题，难于找到一个有效的算法。实际上对于某些顶点数不到100的网络，利用现有最好的算法和计算机也需要比较荒唐的时间（比如几百年）才能确定其是否存在一条这样的路径。

给定图G，若存在一条回路，经过图中每个结点恰好一次，这条回路称作汉密尔顿回路。

狄拉克定理：

Asimple graphwith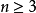 graph verticesin which eachgraph vertexhasvertex degree 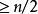has aHamiltonian cycle.2

翻译过来就是：

设一个无向图中有 N 个节点，若所有节点的度数都大于等于 N/2，则汉密尔顿回路一定存在。注意，“N/2” 中的除法不是整除，而是实数除法。如果 N 是偶数，当然没有歧义；如果 N 是奇数，则该条件中的 “N/2” 等价于 “⌈N/2⌉”。

回路的构造证明汉密尔顿回路存在的过程其实就是构造这条回路的过程，分成以下几个步骤：

任意找两个相邻的节点 S 和 T，在它们基础上扩展出一条尽量长的没有重复节点的路径。也就是说，如果 S 与节点 v 相邻，而且 v 不在路径 S → T 上，则可以把该路径变成 v → S → T，然后 v 成为新的 S。从 S 和 T 分别向两头扩展，直到无法扩为止，即所有与 S 或 T 相邻的节点都在路径 S → T 上。

若 S 与 T 相邻，则路径 S → T 形成了一个回路。

若 S 与 T 不相邻，可以构造出一个回路。设路径 S → T 上有 k + 2 个节点，依次为 S、 v1、 v2…… vk和 T。可以证明存在节点 vi， i ∈ [1, k)，满足 vi与 T 相邻，且 vi+1与 S 相邻。证明方法也是根据鸽巢原理，既然与 S 和 T 相邻的点都在该路径上，它们分布的范围只有 v1∼ vk这 k 个点， k ≤ N - 2，而 d(S) + d(T) ≥ N，那么可以想像，肯定存在一个与 S 相邻的点 vi和一个与 T 相邻的点 vj， 满足 j

找到了满足条件的节点 vi以后，就可以把原路径变成 S → vi+1→ T → vi→ S，即形成了一个回路。

现在我们有了一个没有重复节点的回路。如果它的长度为 N，则汉密尔顿回路就找到了。

如果回路的长度小于 N，由于整个图是连通的，所以在该回路上，一定存在一点与回路以外的点相邻。那么从该点处把回路断开，就变回了一条路径。再按照步骤 1的方法尽量扩展路径，则一定有新的节点被加进来。接着回到步骤 2。

编程实现C代码#include#include#include#include#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAX_VER_NUM 11//顶点的最大数#define MAX_ARC_NUM 22//边的最大数typedef char VertexType;typedef int Status;typedef struct EdgeInfo{ VertexType v1; VertexType v2; int weight;}EdgeInfo;typedef struct ArcBox//边所包含的信息{ int iver; struct ArcBox *ilink; int jver; struct ArcBox *jlink; int weight;//权值 int mark; char *info;}ArcBox;typedef struct VerBox//顶点所包含的信息{ VertexType data;//顶点值 ArcBox *firstedge;//指向邻接点（边所包含的信息）}VerBox;typedef struct Graph{ int vernum;//顶点总个数 int arcnum;//边的总个数 VerBox vertexs[MAX_VER_NUM];//顶点信息}Graph;typedef struct StackData//栈中可存放的数据{ VertexType data; int lenght; struct StackData *pnext;}StackData;typedef struct Stack//栈用于存放已访问过的顶点{ struct StackData *ptop; struct StackData *pbottom; }STNODE;typedef struct Stack_Arc//存方已访问过的边及顶点{ ArcBox *p[MAX_ARC_NUM]; int v_num[MAX_ARC_NUM];}SANode;int Visited[MAX_VER_NUM];//标记顶点是否被访问过EdgeInfo Data[MAX_ARC_NUM]={{'A','B',324},{'A','J',419},{'A','K',328},{'A','D',241},{'A','C',556},{'A','F',703},{'A','G',521},{'B','G',391},{'B','H',230},{'B','I',356},{'B','J',220},{'C','F',642},{'C','E',337},{'D','F',829},{'D','K',334},{'E','F',581},{'E','G',1254},{'F','G',887},{'G','H',242},{'H','I',249},{'I','J',713},{'J','K',398}};//边及权值int Count=0;//记可走边的总数STNODE Stack;//存放已访问过SANode Store_Arc_Ver;//存放弧的信息及顶点信息int LAV=-1,ALL=0;int Short_Len=1000000,Short_Load=0;//存放最断最路经void CreateGraph(Graph **G);//创建图int LocateVer(Graph G,VertexType v);//查找顶点v在图中的位置void ShowAdjInfo(Graph *G);//查看邻接点信息int FirstAdjVer(Graph *G,int v,ArcBox **u);//第一邻接点int NextAdjVer(Graph *G,int v,int w,ArcBox **u);//下一邻接点void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u);//递归查找下一邻接点void InitArcBox_mark(ArcBox *p);//初始化mark的值void DFSTraverse(Graph *G);//深度优先遍历图void DFST(Graph *G,int v);//剃归深度优先遍历void InitStack(void);//初始化栈void Push(VertexType c);//数据进栈void Pop(void);//出栈Status IsAdj(int *len,VertexType v);//判断栈顶的点是否与A为邻接点int main(){ Graph *G=NULL; CreateGraph(&G); printf("顶点的邻接表：\n"); ShowAdjInfo(G);printf("\n\n"); printf("可走路径结果:\n"); DFSTraverse(G);printf("\n"); printf("可走路径总数:%d条；最短路径为:路径%d，长度为:%d\n\n",ALL,Short_Load,Short_Len); return 0;}void CreateGraph(Graph **G)//创建图{ int i,j,k,w; char v1,v2; ArcBox *pnew; (*G)=(Graph *)malloc(1*sizeof(Graph)); if((*G)==NULL) { printf("动态内存分配失败，程序终止！\n"); exit(-1); } (*G)->arcnum=MAX_ARC_NUM; (*G)->vernum=MAX_VER_NUM; for(i=0;ivernum;i++) { (*G)->vertexs[i].data='A'+i; (*G)->vertexs[i].firstedge=NULL; } for(k=0;karcnum;k++) { v1=Data[k].v1; v2=Data[k].v2; w=Data[k].weight; i=LocateVer((**G),v1); j=LocateVer((**G),v2); if(i>=0&&j>=0) { pnew=(ArcBox *)malloc(1*sizeof(ArcBox)); if(pnew==NULL) { printf("动态内存分配失败，程序终止！\n"); exit(-1); } pnew->iver=i; pnew->jver=j; pnew->weight=w; pnew->mark=FALSE; pnew->ilink=(*G)->vertexs[i].firstedge; pnew->jlink=(*G)->vertexs[j].firstedge; (*G)->vertexs[i].firstedge=pnew; (*G)->vertexs[j].firstedge=pnew; } else { printf("注意：*****顶点%c不存在！*****\n",i=0;w=NextAdjVer(G,v,w,&u)) { printf("->[%d|%c|%d]",w,G->vertexs[w].data,u->weight); } InitArcBox_mark(G->vertexs[v].firstedge); printf("\n"); }}int FirstAdjVer(Graph *G,int v,ArcBox **u)//第一邻接点{ int w=-1; ArcBox *p; p=G->vertexs[v].firstedge; (*u)=p; if(v==p->iver) { w=p->jver; p->mark=TRUE; } else if(v==p->jver) { w=p->iver; p->mark=TRUE; } return w;}int NextAdjVer(Graph *G,int v,int w,ArcBox **u)//下一邻接点{ int n=-1; ArcBox *p; (*u)=NULL; p=G->vertexs[v].firstedge; NAV(p,&n,v,w,&(*u)); return n; }void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u)//递归查找下一邻接点{ if(p->mark==FALSE && (p->iver==v ||p->jver==v)) { (*u)=p; if(p->iver==v) { *n=p->jver;p->mark=TRUE; } else if(p->jver==v) { *n=p->iver;p->mark=TRUE; } else printf("下一邻接点数据出错，请检查！\n"); } else { if(p->ilink!=NULL && *n==-1) { NAV(p->ilink,n,v,w,&(*u)); } if(p->jlink!=NULL && *n==-1) { NAV(p->jlink,n,v,w,&(*u)); } } return;}void InitArcBox_mark(ArcBox *p)//初始化mark的值{ p->mark=FALSE; if(p->ilink!=NULL) { InitArcBox_mark(p->ilink); } if(p->jlink!=NULL) { InitArcBox_mark(p->jlink); } return;}void DFSTraverse(Graph *G)//深度优先遍历图{ int v; for(v=0;vvernum;v++) { Visited[v]=FALSE; InitArcBox_mark(G->vertexs[v].firstedge); } InitStack(); DFST(G,0); return;}void DFST(Graph *G,int v)//剃归深度优先遍历{ int w=-1,flag=1,i=0,enter=1,len=0; ArcBox *u;//邻接点 StackData *p; Visited[v]=TRUE; Count++; Push(G->vertexs[v].data); if(Count==11&&IsAdj(&len,Stack.ptop->data)==1) { ALL++; printf("路径%-2d：",ALL); printf("A"); p=Stack.ptop; len=len+p->lenght; if(Short_Len>len) Short_Load=ALL,Short_Len=len; while(p!=Stack.pbottom) { printf("->%c",p->data); p=p->pnext; } printf(" 总长度为：%d",len); printf("\n"); } for(w=FirstAdjVer(G,v,&u);w>=0;w=NextAdjVer(G,v,w,&u)) { enter=1; for(i=0;i=0;)//还原当前顶点边的状态并出栈 { Store_Arc_Ver.p[LAV]->mark=FALSE; Store_Arc_Ver.p[LAV]=NULL; LAV--; }}void InitStack(void)//初始化栈{ Stack.pbottom=Stack.ptop=(StackData *)malloc(1*sizeof(StackData)); Stack.pbottom->pnext=NULL; return;}void Push(VertexType c)//数据进栈{ StackData *pnew; char v1,v2; int i; pnew=(StackData *)malloc(1*sizeof(StackData)); pnew->data=c; if(c=='A') { pnew->lenght=0; } else { v1=c; v2=Stack.ptop->data; for(i=0;ilenght=Stack.ptop->lenght+Data[i].weight; } } } pnew->pnext=Stack.ptop; Stack.ptop=pnew; return;}void Pop(void){ StackData *p; p=Stack.ptop; Stack.ptop=p->pnext; free(p);}Status IsAdj(int *len,VertexType v)//判断是栈顶的点是否与A为邻接点{ int i; for(i=0;ib?a:b)using namespace std;typedef long long(LL);typedef unsigned long long(ULL);const double eps(1e-8); char B[1