背景

近三十多年来，数学物理反问题已成为应用数学中发展和成长最快的领域之一，之所以如此在很大程度上是受其他学科与众多工程技术领域的应用中产生的迫切需求所驱动。在实践中，许多反问题可归结为第一类算子方程;而反问题的某些求解方法，例如脉冲谱技术(PST)或广义脉冲谱技术(GPST)及最佳摄动量法等，也常常包含以第一类算子方程的求解作为一个子过程。

反问题顾名思义，反问题是相对于正问题而言的。以前面所举的“盲人听鼓”反问题为例，它的正问题就是要在已知鼓的形状的条件下，研究其发声规律，这在数学物理历史上已经研究在先，而且比较成熟。此时鼓的所有谱都能通过一套算法利用计算机算出来。如何区分某个问题的“正”“反”？这并没有一个严格的标准，但是我们可以粗略地这样理解：世间的事物或现象之间往往存在着一定的自然顺序，如时间顺序、空间顺序、因果顺序，等等。所谓正问题，一般是按着这种自然顺序来研究事物的演化过程或分布形态，起着由因推果的作用。反问题则是根据事物的演化结果，由可观测的现象来探求事物的内部规律或所受的外部影响，由表及里，索隐探秘，起着倒果求因的作用。可以看出，正、反两方面都是科学研究的重要内容。

在遥测和勘探技术中提出了大量的反问题。例如，在地球物理勘探中，通过地震波的测量来判断地球内部的结构或地下矿藏的位置;在无损探伤中,用红外线扫描来探测固体材料中的缺陷；通过测量地面上的牛顿引力势来推断地下金属矿藏的位置、形状和密度;利用X光分层扫描构像来作医学诊断等等，都是在研究对象不能达到或直接接触的情况下，利用特定的物理手段来取得有关解的某些信息，而化为数学上的反问题来处理的。工程技术中的定向设计及系统识别等方面的问题，都属于反问题的范畴。在量子物理中，利用散射资料来反推位势的反散射问题，也是一类有重要意义的反问题。

反问题的提法多种多样，且往往在经典的意义下是不适定的。为了求解各种不同形式的反问题，人们已经提出了一些有效的方法，如拉东变换、反散射方法、最优设计方法以及各种正则化方法等，但是还有很多问题有待进一步的研究。

定义反问题方法是相对正问题求解方法而言的。例如，正问题为已知几何外形求解压力或速度分布，而反问题方法就是根据给定的目标函数，如压力或速度分布，求得对应的几何外形的方法。1

研究现状和进展国外关于反问题理论和方法的研究起步较早，最早期的工作可以追溯到20世纪20年代Hadamard在研究线性偏微分方程的Cauchy问题时对反问题不适定性的陈述和研究。20世纪40年代前苏联院士Tikhonov率领他的工作小组开始了反问题的理论研究。终于在60年代推出了至今仍然广泛沿用的Tikhonov、变分正则化方法。并于70年代出版了反演理论的经典专著《Solutiorrs of lll-posed Problems》 (Tikhorronov et al.，1997；中译本《不适定问题的解法》(王秉忱译，陈恕行校)、地质出版社、1989)，关于反演理论和方法研究的另一个方向是迭代正则化方法，该领域的典型代表是Landweber和Fridman。 以Nashed为代表的广义逆方法是求解反演问题的又一类重要的方法，分为内逆法和外逆法。把不适定问题的正则化放在抽象的泛函空间的完整描述是Morozov的《Methods for solving IncorrectlyPosed Problems》和Croetsch的《The Theory of Tikhonoy regulation for Fredhohn Equations of the First Kind》近年来发展起来的方法有梯度型方法和Newton方法等等。

我们国家的研究工作者在反演问题的理论和方法研究方面也进行了大量的探索，最早可追溯到20世纪70年代初由中国科学院院冯康先倡导的反演问题的研究。随后，有关反演理论和方法在相关的领域也如火如茶地展开。有对地球物理中的反问题的系统理论论述，有对波动方程反演问题的理论和算法的系统研究，有从控制和脉冲谱角度对反演问题的论述等等、特别是大量科研人员投入精力对反演问题的正则化理论进行研究和扩展，以及从最优化角度对反演理论和方法的研究。2

正则化方法正则化(regularization)，是指在线性代数理论中，不适定问题通常是由一组线性代数方程定义的，而且这组方程组通常来源于有着很大的条件数的不适定反问题。大条件数意味着舍入误差或其它误差会严重地影响问题的结果。

求解不适定问题的普遍方法是:用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,这种方法称为正则化方法。如何建立有效的正则化方法是反问题领域中不适定问题研究的重要内容。通常的正则化方法有基于变分原理的Tikhonov 正则化、各种迭代方法以及其它的一些改进方法,这些方法都是求解不适定问题的有效方法,在各类反问题的研究中被广泛采用，并得到深入研究。

压气机叶片反问题设计反问题设计方法通过给定特定流场参数分布，根据流场参数和几何参数之间的关系求解叶片造型，具有较高的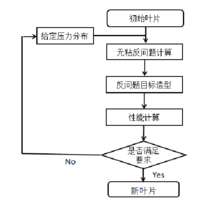设计效率。冯·卡门研究所发展出基于渗透边界的叶片反问题设计方法，给定叶片吸力面和压力面压力分布，反问题计算过程中叶片表面出现渗透速度，在计算收敛的流场中追踪流线实现对新气动型面的求解，以轴流压气机叶片和涡轮叶片为算例验证了其有效性。

叶轮机械内部宏观流动的主要驱动力是压力场，叶表静压直观地反映叶片段的负荷分布，以叶片吸力面、压力面表面压力分布作为给定参数，可实现对叶表流动状态的直接控制。从初始叶片出发，以叶片表面压力作为给定参数的压气机叶片无粘反问题设计流程如下:

1)给定初始叶片及目标压力分布;

2)基于可渗透壁面边界条件的无粘反问题流场计算;

3)反问题目标叶片求解，在反问题流场中计算叶片修正量，得到目标叶片;

4)对目标叶片进行性能计算，叶片表面为固壁边界条件，如果不满足性能要求，则以此叶片作为初始叶片返回至第1}步再进行以上过程，直至得到的新叶片满足目标性能要求。

该反问题方法的主要设计步骤包括基于可渗透壁面边界条件的CFD流场计算和基于流线追踪的壁面求解。无粘正问题计算过程中壁面采用无粘滑移边界条件，叶片表面被视为无流体穿过的物理边界，边界上流体的法向速度为零，仅存在切向流动;无粘反问题计算过程中壁面采用可渗透壁面边界条件，叶片表面被视为流体可穿过的数值边界，边界上流体的法向速度不再必然为零，其方向和数值由流动状态和给定压力的关系决定，从而形成与边界几何上不一致的近壁流线。

流线追踪过程从前缘滞止点出发，基于单元体质量守恒原理求解流线。对于轴流压气机叶片，在正问题无粘流场中，贴体流线与壁面吻合较好;反问题流场中由于壁面法向速度的存在，近壁面流线不再与壁面重合，可基于此原理追踪从前缘滞止点出发的流线(或流面)，以此作为与给定压力分布相匹配的新叶片壁面可实现反问题设计。3