背景

图像边缘包含了图像最重要的信息。所谓边缘一般是指图像灰度变化率最大的集合， 所以边缘广泛存在于物体与背景之间、物体与物体之间、基元与基元之间。由于图像边缘包含了大量的图像的重要信息，因此，图像边缘检测成为图像处理的一个重要环节。

目前国内外对图像边缘检测有着比较广泛的研究，经典的边缘检测算子常借助空域微分算子进行，通过微分模板与图像卷积完成。常见的边缘算子有 Roberts、Sobel、Prewitt和Krisch 等，其中 Sobel 算子[1] 检测速度快， 是实践中最常用的算子；但是 Sobel 算子通过阈值对梯度场进切割得到图像边缘，阈值过大会造成边缘的丢失，阈值过小又会造成一些非边缘点当成边缘点被分割出来进而形成伪边缘。

近年来随着数学理论和人工智能的不断发展，许许多多新的边缘检测方法被提出。基于小波变换的图像边缘检测具有能避免噪声干扰的特点，但会丢失一些弱边缘；基于模糊理论的边缘检测算法具有较的抗噪能力， 但矩阵变换的运算较为复杂；基于蚁群算法的边缘检测对噪声有良好的免疫作用，但会丢失一些边缘信息。

传统的图像边缘检测算子一般都只能得到多像素宽边缘，这为后续的图像处理带来了一定困难。正由于边缘细化算法较为重要，因此其一直以来都得到学者的关注，并已取得了一定的研究成果。现有的边缘细化算法可粗略地分为两大类：基于二值边缘图像的方法和基于数学形态学的方法 。

细化方法所谓细化，通常是把一个具有一定面积的区域用一条曲线来代表它。边缘细化，即为把较粗的边缘用一条较细的曲线来表示。

基于数学形态学数学形态学细化算法的主要思想是源于击中击不中变换的形态学算法。在给定一系列具有一定形状的结构元素后，顺序循环地删除满足击中变换的像素。

所谓细化，就是寻找图形、 笔划的中轴线或骨架， 以其骨架取代该图形或笔划。 在遵循对图像的细化要保持图像连通性的最基本原则下，细化之后的图形或笔划的像素宽度为 1。 细化过程也就是对图像逐层剥落的过程，随着细化的进行，图像有规律地缩小。 数学形态学基本运算中的薄化，即 AOB，可以使图形按一定规律不断缩小， 并始终保持 。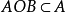

结构元素 B的选择尤为重要，是影响细化质量的关键因素。 细化算法将不断重复地剥离二值图像的边界像素。但是， 对于边界像素的剥离应保持目标图像纹线的连接性，方向性和特征点不变，还应保持纹线的中心基本不变，最终使得变换图像成为单像素宽的图像骨架。

下面举例说明：

考虑以上因素，采用图 1所示结构元素。其中，符号 “*”表示既可取灰度 1，又可取灰度 0的像素。然后将这两种结构元素 (a)、(b)陆续旋转 90°、180°和 270°，得出 6 种结构元素, 共有8种结构元素。这 8种结构元素分别对应着东、西、南、北及东北、西北、西南及东南8个方向上的边界点。

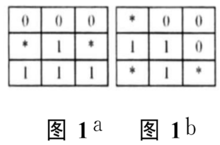
结构元素确定后，利用形态学中的薄化运算对图像进行细化。1

基于二值边缘图像图像细化就是从原来的图像中去掉一些点，但仍要保持目标区域的原来形状。二值边缘图像细化即是判断原边缘上每一像素点是否应被剔除，以此来一层层剥离原边缘最外层的伪边缘。

以HSCP边缘细化算法2为例。

首先给出图像中像素点 8 连通域示意图，下图所示。则HSCP 算法可简述如下：

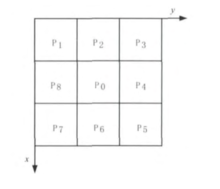
Step1：针对所有的边缘点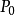 ，若满足如下条件，则判断其为待剔除点。

（1）其 8 连通域中的边缘点数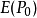 满足: ；
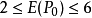( 2) 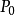的 8 连通域包含且只包含一个 4 连通边缘点。

Step2：遍历所有的待剔除点， 若满足如下条件之一，则保留，否则删除。

（1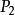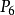） ， 为边缘点，但 为待剔除点；
（2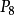） ， 为边缘点，但 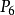为待剔除点；
（3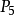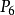） ， ， 均为待剔除点。

以上两步操作构成一次迭代，不难发现，在每次迭代中需两次循环遍历，首先需遍历全部边缘点，判断是否为待剔除点; 然后再次遍历全部待剔除点，再次判断这些点是否确实可剔除， 目的是防止过多地剔除边缘细节， 保持原有边缘的连续性。此算法计算量较大。

上述算法被指出3具有两个缺陷：
（1）保留了孤立的边缘点。因为孤立点 8 邻域内非零点的个数为 0，即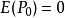 ， 而待剔除点必须满足 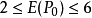，所以孤立点未被剔除。
（2）运算量较大。采用两层循环构成一次迭代，尽管每次迭代对象不尽相同，算法开销依然较大

三个性质一个性能良好的边缘细化算法应该具有如下三个性质4：
（1）单像素宽细化结果

理想的算法应该能给出单像素宽的细化结果 。
（2）保持边缘的原有信息

边缘细化结果不能改变边缘的原有信息，即边缘的连通和走向趋势， 因为这些信息是进行图像理解、目标识别的重要依据。

（3）计算开销小
能被实际广泛运用的算法自然是计算开销小 、执行效率高的方法