定义
切尔诺夫限,也称为切尔诺夫不等式,是关于一组独立随机变量和的一类概率不等式.。是由赫尔曼-切尔诺夫而命名的。然而,切尔诺夫约束要求变量是独立的,而与之相类似的马尔科夫限和切比雪夫限都不需要。
证明对于随机变量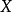 定义的通用切尔诺夫不等式通过将马尔可夫不等式应用于
定义的通用切尔诺夫不等式通过将马尔可夫不等式应用于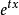 来获得,对于每一个
来获得,对于每一个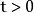 ,
,
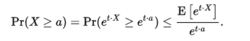
当是n个随机变量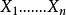 的时候,我们得到任何
的时候,我们得到任何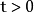 ,
,
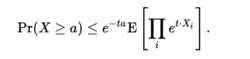
优化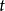 并使用
并使用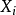 独立的假设,
独立的假设,
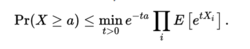
同样的,
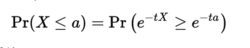
所以,
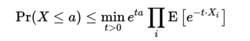
命题得证,以上不等式的一个重要意义在于,我们仅仅知道随机变量的数字特征便可以得到概率的界1。
示例令X1,...,Xn是独立的伯努利随机变量,其总和为X,每个都具有等于1的概率p> 1/2。对于伯努利变量,
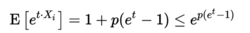
所以,
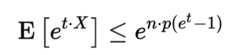
对于任何的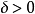 ,由
,由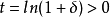 和
和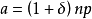 可得,
可得,
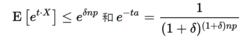
利用切尔诺夫不等式可得,
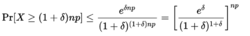
同时发生事件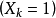 的
的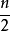 以上的概率具有精确的值,
以上的概率具有精确的值,
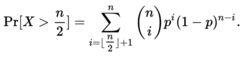
这个概率的下限通过切尔诺夫不等式来计算,
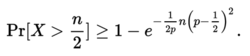
最后得出,
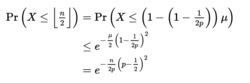
绝对误差(加法形式)以下定理是瓦西里·霍夫丁提出的,所以称为切尔诺夫-霍夫丁定理。
假设X1,...,Xn是随机变量,取{0,1}中的值。令p = E [ X i ],ε > 0。然后,
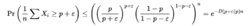
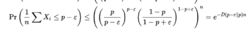
由于,
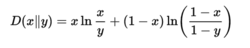
所以
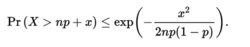
相对误差(乘法形式)假设X1,...,Xn是随机变量,取{0,1}中的值。令X表示他们的和,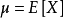 表示和的预期值,对于任何
表示和的预期值,对于任何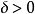 ,
,
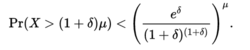
类似的证明出,
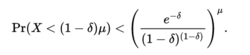
上述公式在实践中往往不方便,因此常常使用以下更简单方便的界限:
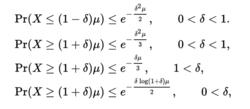
应用设计统计实验时出现设定的平衡问题。通常在设计统计实验时,考虑到实验中每个参与者的特征,我们需要知道如何将参与者分成两个不相交的组,使得每个特征在两组之间尽可能大致相等。
切尔诺夫限也用于获得排列路由问题的紧密界限,在减少网络拥塞的同时稀疏网络中路由数据包。
切尔诺夫限可以有效地用于通过随机化探索其扰动空间来评估应用算法的“鲁棒性”级别。使用切尔诺夫限放弃不切实际的小扰动假设(扰动幅度很小)。鲁棒性级别又可以用于验证或拒绝特定的算法选择,硬件实现或其结构参数受不确定性影响的解决方案的适当性。


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

