圆形音圈电机能够直接产生直线运动，在驱动系统中不需要皮带、齿轮等中间传动机构，大大降低了能量损耗，节约了成本，并极大地提高了系统的响应速度和控制精度1。然而业界对音圈电机的详细设计步骤介绍的却不是太多，并且在进行音圈电机的磁路设计时，设计人员的经验是一重要因素。另外，虽然永磁材料发展速度很快，性能越来越高而且价格逐步降低，但是在永磁电机的造价中，永磁材料仍然占有很大的比重。通过合理设计音圈电机的磁路结构，使用较少的永磁材料，在电机工作气隙中产生满足要求的磁通密度就显得很有必要2。

永磁励磁音圈电机结构

根据运动部件的不同，音圈电机可分为动铁式和动圈式结构；根据音圈电机内线圈的长短可分为长音圈型和短音圈型；根据永磁体的不同位置可分为外磁式结构和内磁式结构；根据运动方式的不同，音圈电机可分为直线型和摆动型两类。根据其外形又可分为：圆柱形、扁平形、圆形（含弧形）、扁平形等不同种类3。

（1）动圈式和动铁式结构

按照音圈电机中运动的是音圈还是铁磁系统，可将音圈电机分为动圈式和动铁式两种类型。

在动圈式结构中，可以将铁磁系统做的大一些，以便产生所需要的气隙磁通密度。音圈是运动部件，在电力系统中容易出现故障，并且工作时产生的热量不容易消散，所以在音圈中的电流不能太大。其优点运动部分质量小，惯性也小，动态响应好。

动铁式结构中，由于铁磁系统在运动，所以对永磁体的体积、重量都有要求。在设计时需要一个较长的固定的线圈，结构比较复杂，且运动部分重量大，惯性也大，故其动态响应没有动圈式好。其优点是散热容易，线圈中可以通较大的电流，行程也可以做的很长。

（2）长音圈和短音圈结构

音圈电机按照其工作气隙与音圈长度的大小关系，可分为长音圈结构VCM和短音圈结构VCM。

长音圈结构VCM的音圈长度≥工作气隙长度+最大行程长度，其优点是永磁体体积较小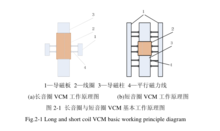，能够充分利用永磁体产生的气隙磁通密度，节省了成本。缺点是线圈较长，只有少部分工作在气息中造成电能浪费，导磁板端部漏磁较多。其基本工作原理图如图2-1(a)所示：

短音圈结构VCM的音圈长度+最大行程长度≤工作气隙长度，其优点是线圈长度较短且全部都工作在气隙中，电能利用率高，功耗容易控制。相比于长音圈结构VCM，其导磁板较大。其基本工作原理图如图2-1(b)所示：

（3）外磁式结构和内磁式结构

永磁音圈电机按照永磁体的位置可以分为外磁式VCM和内磁式VCM。外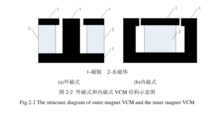磁式结构：当永磁体在工作气隙外部的时候为外磁式结构。为了减少磁体内部损耗，一般将高矫顽力的永磁材料做成面积大而厚度小的环形磁体，这样能大大提高磁能的利用。对于需要在音圈电机中间穿孔的场合，适宜采用这种结构。其结构示意图如图2-2(a)所示。

内磁式结构：当永磁体在工作气隙内缘时为内磁式结构。其优点是磁路较短，能充分利用永磁体的磁力线，漏磁通量比较小。其结构示意图如图2-2(b)所示4。

（4）其他结构类型

音圈电机还有很多分类方式，根据运动方式的不同，可分为直线型和摆动型两类，如在硬盘中驱动磁头摆动的就是摆动型音圈电机。根据音圈电机的外形结构又可分为：圆柱形、扁平形、圆形（含弧形）、扁平形，如图2-3所示。

为了明确影响音圈电机性能的因素， 需要建立音圈电机在工作时的数学模型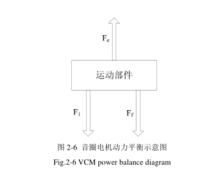，才能对音圈电机深入认识，并针对影响其性能的相关因素进行优化2。

由音圈电机的工作原理可知在其工作时，线圈上产生的电磁力为：

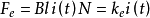式中： B 为 VCM 工作气隙的磁感应强度 （T） ，l 为音圈每匝在气隙中的有效长度 （m），i为线圈内电流的大小（A） ，N 为线圈匝数，ke=BlN。

为了使线圈运动，电磁力 Fe应大于最大静摩擦力与负载阻力之和。其动力学模型如图 2-6 所示，由图可以得到音圈电机工作时的动力平衡方程：

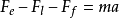
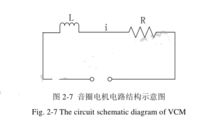式中：Fe为电机产生的电磁力，Fl为负载阻力，Ff为滑动摩擦力，m 为运动部件的质量，a 为运动部件的加速度。

由音圈电机的工作原理，可以画出音圈电机工作时的电路结构示意图 2-7：

音圈电机工作时的电压平衡方程为：

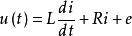
式中：u为音圈电机工作时的电压，L为电路的电感，i为电路中的电流，R为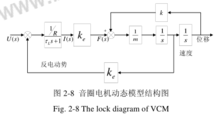电流回路的电阻，B为音圈所在气隙的磁感应强度，e为音圈在磁场中的运动时产生的反电动势，其方向总是与电流方向相反。

e的大小可以推知为：

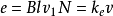
式中，v为音圈在磁场中的运动速度。

加速度a，速度v以及位移x之间的关系为：

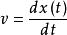
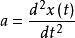
为了研究影响音圈电机工作性能的主要因素，可以忽略空气阻尼和摩擦力，可以分别得到动力平衡方程：

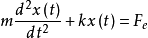
式中：c为阻尼系数，k为弹簧的劲度系数。

电压平衡方程

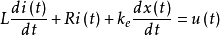
将上两式的中间变量Fe、i(t)、e消去，可以得到电压为输入量，位移为输出量的系统微分方程：

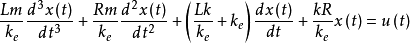
可以画出音圈电机的动态模型结构图如图2-8所示。图中ke=BlN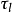，是线圈的电磁时间常数，。

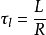在实际运行中，电感非常小，并且音圈电机驱动熄火拉线时是低频运动，可以忽略电感的影响，则音圈电机的电压—位移的数学模型变为：

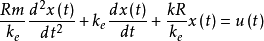
对上式进行拉普拉斯变换，可以得到系统传递函数：

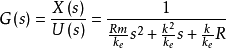
音圈电机驱动系统是一个二阶系统，机电时间常数为：

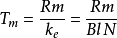
Tm是一个重要参数， 它的大小会影响到音圈电机的响应速度。 通过分析知道，提高气隙磁通密度B，减少运动部件的质量可以减少机电时间常数Tm，提高系统响应速度2。