简单概述

应用含时微扰理论可以近似的计算出有微扰时的波函数，从而计算无微扰体系在微扰作用下由一个量子态跃迁到另一个量子态的跃迁概率。含时微扰包括常微扰和周期微扰，在这两种微扰作用下，得到的结果是不同的。

含时微扰理论可以通过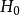 的定态波函数近似的求出微扰存在情况下的波函数，从而可以计算无微扰体系在加入含时微扰后，体系由一个量子态到另一个量子态的跃迁机率。

在有关量子跃迁的问题中，含时微扰理论给出了跃迁概率振幅的一级近似解。若微扰只与时间有关，则体系的波函数可以精确求解，从而得到跃迁概率振幅的精确表达式。12

分类常微扰在常微扰作用下时，可以得到了一个重要公式，即费米黄金定则。常微扰是只在一段时间内起作用，时间足够长的话，则跃迁概率与时间无关。

周期微扰通过计算无微扰体系在周期微扰作用下的跃迁概率，可以发现周期微扰的频率只有在一定范围内，才会发生跃迁。只有当外界微扰含有频率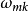 时，才会出现明显跃迁。

对体系产生的效果如果微扰作用平缓稳定，则将产生定态扰动效果，如能级与量子态偏移，简并消除等。如果扰动作用是以淮静态方式加于体系的（即变化极其缓慢），将不会产生跃迁效应。相反，若扰动作用时间不长，则只可能发生跃迁而不会发生定态扰功效应。对于一般情况，两种效应都可能发生。这里，扰动时间长短，或变化快慢，是相对体系本身的所谓特征时间而言的。如对于原子，其特征时间为（秒）。因此，人为施加的宏观扰动都可视为定态扰动（为体系能级间距所对应的角频率）。2

应用光的发射和吸收光的发射和吸收是光谱学所要讨论的主要过程，而这些过程中所涉及的吸收系数、发射和吸收截面、振子强度等概念和有关的计算公式是激光材料光谱和激光性能研究中经常要用到的。因此，从电动力学和量子力学的基本原理出发,比较系统地叙述这些概念并推导出相关的计算公式是必要的。在讨论中，我们把概率论的全概率公式应用到光跃迁几率的计算中，对各向异性介质中的跃迁几率计算给出比较清晰的论述。另一方面也给出振子强度的正确定义。

选择定则微观粒子在不同的量子化状态间变化，称为跃迁。跃迁有很多种，不同跃迁遵从不同的跃迁选择定则。原子辐射跃迁的选择定则是原子能级之间发生跃迁所满足的条件，它对于研究光的吸收和发射具有很重要的意义。由于电偶极矩跃迁强度比其它形式的跃迁强度大很多倍，原子的辐射跃迁选择定则是指电偶极辐射跃迁选择定则。它是从大量光谱的观察分析和研究中总结出来的。