简介

水灰比定律是1 9 1 8 年美国波特兰水泥协会( PCA ) 创建初期的混凝土专家阿伯拉姆氏提出的。这个定律影响深远, 几乎每一个混凝土工作者都能背诵: “ 在一定的材料和试验条件下, 只要混凝土混合物是塑性的, 混凝土的强度则取决于拌和水的数量” , 其公式为: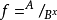 ,式中,f为6英寸直径、12 英寸高（15*30厘米）圆柱体试件的抗压强度, A 和B ——常数, 随水泥质量、龄期、养护、试验等方法不同而不同, X ——水灰比( w / c ) , 按体积计。

1 9 3 4年波特兰水泥协会重申水灰比定律应是: “ 在一定的工作条件下, 集料品质和配合比不变时, 塑性混凝土的强度与其它性质, 都可由水灰比决定” 。而后又将水灰比值从体积比改为重量比。

直到上世纪八十年代, 这个定律一直在世界各国的混凝土界沿用着, 但是也一直被许多混凝土学者议论着。最近在有些国家似乎又出现议论的热潮。我们对于这些议论, 也不能当作街谈巷议而等闲视之, 若是认真分析一下, 也许能从中寻觅到一些有用的材料。1

水灰比定律的实效严格地说, 阿伯拉姆氏的水灰比定提出时, 已有足够多的实验数据, 并制成系统的曲线, 导出可以定量的公式, 但与其它自然科学一般的定律比较, 容易发现它的破绽, 似乎还不足以达到称之为定律的程度。比如, 当时阿伯拉姆氏认为混凝土强度与集料的粒径和用量都无关系, 只有当集料的性质影响到混凝土的需水量时, 才能间接地影响混凝土的强度; 后来有人就从这一点出发, 指出在水灰比定律中过于简化了影响混凝土强度的各项因素的关系, 特别是忽视了集料的作用。

其实, 对水灰比定律提出的种种指责, 都还没有从根本上撼动这个定律在实用中的地位。但看水灰比定律的形成过程: 阿伯拉姆氏是为混凝土配合设计的要而提出来的, 有人评论当时阿伯拉姆氏对混凝土技术一举作出三大贡献, 一是水灰比定律, 二是细度模数配合设计法, 三是坍落度试验法; 但是比较成功的只有两个半。其中水灰比定律和坍落度试验两者一直被沿用, 当然是属于成功的, 但是细度模数配合设计法却嫌不够简捷, 而用细度模数估计细集料的粗细程度, 大家还认为有一定的实用价值, 只能算半个。因此说多少年来实践考验证实, 用水灰比定律的公式, 估算混凝土强度, 用水灰比最大限值, 保证混凝土耐久性, 确是简单而有实际效益的。再从近代理论上说, 水泥浆体的强度取决于水灰比和水泥的水化程度, 但水化程度相同的水泥浆体, 其强度就主要取决于水灰比。至于混凝土的强度, 固然是取决于水泥浆体的强度, 还有浆体和集料界面的结合强度, 也还有集料的影响。浆体强度既取决于水灰比, 同时水灰比也对界面强度起决定性的作用, 因此说, 若不考虑集料的影响, 那么混凝土的强度还是主要取决于水灰比。再说一般集料的强度总是远远超过水泥浆体的强度, 于是在普通混凝土中集料对混凝土强度影响的程度是有限的, 所以对于集料最大粒径在一定范围内(10~ 30 毫米) 的普通混凝土的强度而言, 水灰比仍是主要的影响因素。当然, 采用粒径较大的粗集料或者应用轻集料时, 水灰比与强度的关系式中, 常数A和B , 就要加以修正了。这样, 从实效来看, 可以认为阿伯拉姆氏独具慧眼, 是首先识别水灰比实用价值的重要历史人。

水灰比定律发展史现阶段的水灰比与强度的关系式也并非完全来自阿伯拉姆氏的水灰比定律, 试举下列一些我们比较知名的混凝土学者所提出的水灰比关系式便可说明。

( l ) 别辽也夫公式苏联别辽也夫在3 0年发表的双曲线型水灰比公式, 基本与阿伯拉姆氏公式相同: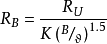

式中,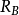 — 混凝土的抗压强度, 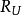——水泥的标号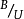， ——水灰比（重量比），K——常数，用碎石时是3.5，用砾石时为4.0。此式将水泥标号这个因素, 从常数中分列出来, 而常数值成为粗集料因素, 由于计算时仍嫌麻烦, 实际上是利用绘制的关系曲线或查表方法。

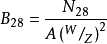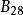( 2 ) 格拉夫公式德国的格拉夫在1 9 3 0年前后, 建议采用以下公式: ,式中, ——混凝土28 天抗压强度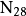， ——水泥标号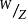， ——水灰比(重量比），A——常数，4-8.此式与别辽也夫公式的区别, 仅在于德国采用的水泥试验方法与当时苏联硬练砂浆试验不同。

( 3) 雷芝公式当保罗米公式在欧洲传播之际, 无独有偶的事情发生了, 即著名的挪威混凝土学者雷芝将阿伯拉姆氏公式演变为与保罗米公式几乎雷同的直线关系式, 在美国广为流传, 称为雷芝灰水比公式: .

保罗米公式或雷芝公式异途同归, 便于实用, 从此许多国家各自发展了适合国情的灰水比公式, 列人规程; 或者有些大型工程或混凝土工厂, 根据试验结果, 过数理统计处理, 自列“ 经验公式” , 只不过常数不同而已.

( 4 ) “ 水泥空间比” 学说美国泰尔博特等最初也是根据菲莱” 特水泥空隙比理论, 发表了“ 水泥空间比公式: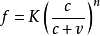 .上式中所谓水泥空间比, 实际上是单位体积的新拌混凝土中水泥的绝对体积与水泥浆的绝对体积之比, K = 2250公斤/平方厘米“ , n = 2.5。泰尔博特强调了混凝土结构中空隙的重要影响, 又提出了“ 基准水量” 和“ 相对水量” 等观点和实验数据, 更进一步接近现代混凝土强度理论,可是尽管当时在理论上领先, 而他们所建议的方法应用时必需建立四个关系曲线,相当费事, 终于不能普遍推广。菲莱特和阿伯拉姆氏两说, 最初看来“ 各有于秋” , 最后终于“ 合二为一” ,我们还应归功于众多的孜孜不倦的混凝土技术领域的耕耘者, 同时也不应忘记混凝土技术历史上的那段从启蒙到发展的鼎盛春秋。2

近代发展情况1 . “ 胶空比” 学说

恰恰是在当年阿伯拉姆氏所在的那个美国波特兰水泥协会中, 以后有个成为该会主要学者的鲍威斯, 并不追随阿伯拉姆氏的水灰比定律, 却发展了与菲莱特的水泥空隙比学说一脉相承的“ 胶空比” 学说, 并考虑到了水泥水化程度( 参阅现代混凝土技术特写之二“ 水泥浆体和微混凝土”)试将胶空比公式进一步分析, 不难发现, 新拌水泥浆体的初始空隙率仍然是主要取决于水灰比, 即浆体中的相对水量。新拌水泥浆体的体积, 等于水泥和拌和水体积之和, 算式如下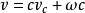 :式中,c——水泥的用量; 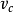——水泥的比容( 比重的倒数) , 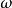——水灰比。而初始空隙( Pi ) 的算式是: 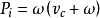当然, 水泥浆体的空隙与水化程度有关, 但在同一水化程度条件下, 水泥浆体的空隙率取决于初始空隙, 也即取决于水灰比。这样表明水泥浆体强度与水灰比的关系, 完全类似强度与空隙率的关系。根据这样的关系所绘成的水泥浆体强度S( 以对数表示) 与相应水灰比的直线关系图, 即10 9 5 = A 一B (W / C ) , 它与阿伯拉姆氏的水灰比公式关系图, 几乎一模一样, 也说明了胶空比学说与水灰比定律密切的血缘关系。

2.引气穿昆凝土的水灰比

有人提出, 水泥空隙比学说较适用于引气混凝土, 而近年研究结果, 表明水灰比定律的公式略加补充, 也可妥善解决这个问题。即引气混凝土的水灰比可写成( W 十△A )/ C。一般情况下, 即使是捣实程度较好的普通混凝土, 也会含有一部分空气量, 通常由于集料的最大粒径的不同, 这部份空气量为10 ~ 30 升/ 立米, 混凝土中最佳含气量变化范围为45 ~ 65 升/立米, 因此通常△A = 35 升/ 立米。2

3 . 模式的突破

许多人指出水灰比定律在实用中最大的缺点就是在理论上水灰比定律是以均匀的混凝土结构为前提, 而实际上由于泌水和粗集料的沉降作用在往会引起不均匀现象。为此学者们强调引气剂的作用,呼吁大家注意当前只重推广减水剂而忽视引气剂的状况。此外, 日本混凝土工程界正在积极发展“ 灰浆裹砂混凝土” (S E C混凝土) , 其原理是使用专门的砂料控制器, 将砂的含水量控制在恒定的范围内,再将带有适量表面水份的砂子, 与水泥、粗集料共同搅拌, 于是水泥就粘着在砂粒的表面上, 形成一层水灰比较小的水泥浆表壳, 然后再加入其余的拌和水量以及必需的外加剂, 最后搅拌成灰浆裹砂混凝土。在这种混凝土中水灰比较小的水泥浆壳砂粒互相粘连起来, 可以把水灰比和流动性较大的稀浆体, 封闭在砂粒间的空隙中。裹砂的灰浆水灰比在0.15 至0.25 之间, 如用流变学原理解释, 水灰比过低不能包满砂粒, 水灰比过高则发生流淌。试验结果表明, 不仅由于砂粒间粘结强度提高而使混凝土强度提高, 而且会在流动性较大的情况下, 几乎一点也不发生泌水和集料沉降现象。它还适用于喷射混凝土。有人认为此法对水灰比定律有所突破, 但考其实质, 关键在于降低了砂粒表层灰浆水灰比, 也即提高了浆体和砂粒的界面结合强度, 这方面仍是受到水灰比定律支配的。但是对原来的水泥浆体均匀分布的式有所突破。1