定律定义
设函数项级数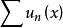 定义在数集
定义在数集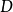 上,
上, 为收敛的正项级数,若对一切
为收敛的正项级数,若对一切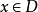 ,
,
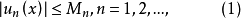 则函数项级数数
则函数项级数数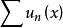 在
在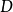 上一致收敛1.
上一致收敛1.
推导过程由假设正项级数 收敛,根据数项级数的柯西准则,任给正数
收敛,根据数项级数的柯西准则,任给正数 ,存在某正整数
,存在某正整数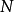 ,使得当
,使得当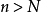 及任何正整数
及任何正整数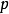 ,有
,有
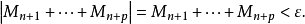 又由(1)式对一切
又由(1)式对一切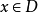 有
有
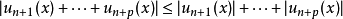
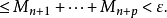
根据函数项级数一致收敛的柯西准则,级数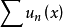 在
在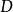 上一致收敛.
上一致收敛.
应用领域例函数项级数
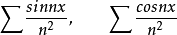 在
在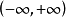 上一致收敛. 因为对一切
上一致收敛. 因为对一切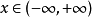 有
有

而正项级数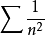 是收敛的.
是收敛的.
魏尔斯特拉斯定理也称为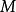 判别法或优级数判别法. 当级数
判别法或优级数判别法. 当级数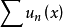 与级数
与级数 在区间
在区间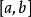 上成立关系式(1)时,则称级数
上成立关系式(1)时,则称级数 在
在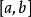 上优于级数
上优于级数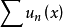 ,或称
,或称 为级数
为级数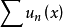 的优级数.
的优级数.


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

