如果函数f在点x连续,则称x是函数f的连续点;如果函数f在点x不连续,则称x是函数f的间断点。
定义设函数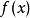 在某
在某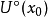 上有定义。若
上有定义。若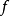 在点
在点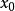 无定义,或
无定义,或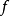 在点
在点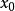 有定义而不连续,则称点
有定义而不连续,则称点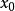 为函数
为函数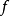 的间断点或不连续点。
的间断点或不连续点。
若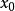 为函数
为函数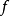 的间断点,则必出现下列情形之一:
的间断点,则必出现下列情形之一:
(i)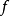 在点
在点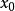 无定义或极限
无定义或极限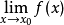 不存在;
不存在;
(ii))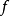 在点
在点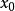 有定义且极限
有定义且极限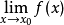 存在,但
存在,但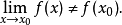
据此,我们对函数的间断点作如下分类1:
可去间断点若
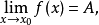
而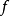 在点
在点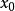 无定义,或有定义但
无定义,或有定义但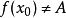 ,则称
,则称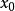 为
为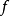 的可去间断点。
的可去间断点。
例如,对于函数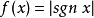 ,因
,因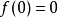 ,而
,而
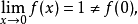 故
故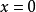 为
为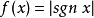 的可去间断点。又如函数
的可去间断点。又如函数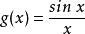 ,由于
,由于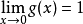 ,而
,而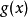 在
在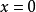 无定义,所以
无定义,所以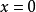 是函数
是函数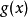 的可去间断点。
的可去间断点。
设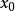 为函数
为函数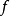 的可去间断点,且
的可去间断点,且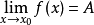 。我们按如下方法定义一个函数
。我们按如下方法定义一个函数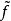 :当
:当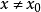 时,
时,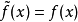 ;当
;当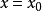 时,
时,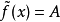 。易见,对于函数
。易见,对于函数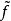 ,
,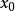 是它的连续点。例如,对上述的
是它的连续点。例如,对上述的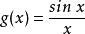 ,我们定义
,我们定义
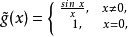 则
则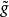 在
在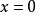 连续。
连续。
若函数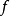 在点
在点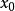 的左、右极限都存在,但
的左、右极限都存在,但
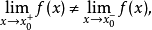 则称点
则称点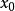 为函数
为函数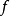 的跳跃间断点。
的跳跃间断点。
例如,对函数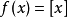 ,当
,当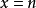 (
( 为整数)时有
为整数)时有
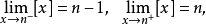 所以在整数点上函数
所以在整数点上函数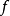 的左、右极限不相等,从而整数点都是函数
的左、右极限不相等,从而整数点都是函数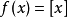 的跳跃间断点。
的跳跃间断点。
可去间断点和跳跃间断点统称为第一类间断点。第一类间断点的特点是函数在该点处的左、右极限都存在。
第二类间断点函数的所有其他形式的间断点,即使得函数至少有一侧极限不存在的那些点,称为第二类间断点。
例如,函数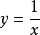 当
当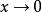 不存在有限的极限,故
不存在有限的极限,故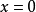 是
是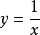 的第二类间断点。函数
的第二类间断点。函数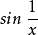 在点
在点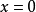 处的左、右极限都不存在,故
处的左、右极限都不存在,故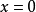 是
是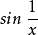 的第二类间断点。当趋近于
的第二类间断点。当趋近于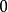 时,函数在
时,函数在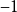 和
和 之间取值,这样的间断点称为振荡间断点。
之间取值,这样的间断点称为振荡间断点。
无穷间断点和振荡间断点都属于第二类间断点。
便于理解和记忆,间断点的分类概括如下:
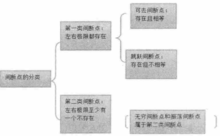
(1)狄利克雷函数2
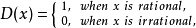 在定义域
在定义域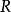 上每一点
上每一点 都是第二类间断点。
都是第二类间断点。
(2)函数
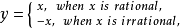 仅在点
仅在点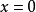 连续,
连续,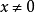 时是第二类间断点。
时是第二类间断点。
(3)整数部函数
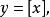 与小数部函数
与小数部函数
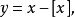 都是在
都是在 为整数时是第一类不可去间断点,在这些点仍是右连续的。
为整数时是第一类不可去间断点,在这些点仍是右连续的。
(4)黎曼函数
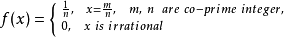 在每一个无理点都连续,而在异与零的有理点都不连续。
在每一个无理点都连续,而在异与零的有理点都不连续。
(5)函数
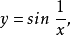 在点
在点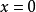 附近函数振荡而无极限,
附近函数振荡而无极限,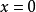 是它的第二类间断点。
是它的第二类间断点。
(6)函数
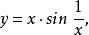 在点
在点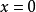 是可去间断点,并且
是可去间断点,并且
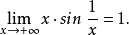
(7)函数
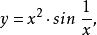 在点
在点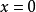 是可去间断点。
是可去间断点。
(8)函数
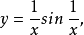 在点
在点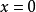 是第二类间断点。
是第二类间断点。
例1 求分段函数
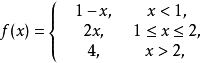 的间断点并判断其类型。
的间断点并判断其类型。
解 因为
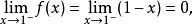
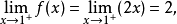
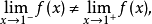
所以,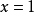 是
是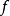 的跳跃间断点。
的跳跃间断点。
又因为
 所以
所以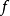 在
在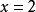 处连续。
处连续。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

