概念
纽马克-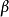 法是一种将线性加速度方法普遍化的方法。纽马克-
法是一种将线性加速度方法普遍化的方法。纽马克-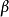 法可认为是概括了平均常加速度和线性加速度算法的一种广义算法。纽马克-
法可认为是概括了平均常加速度和线性加速度算法的一种广义算法。纽马克-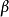 法有拟静力增量方程形式和不同类型的拟静力全量方程形式。在有限元动态分析中最常用的有中心差分法、纽马克-
法有拟静力增量方程形式和不同类型的拟静力全量方程形式。在有限元动态分析中最常用的有中心差分法、纽马克-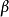 法(Newmark)和威尔逊-θ法。1
法(Newmark)和威尔逊-θ法。1
基本原理纽马克法是对线性加速度假定做了修正,在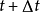 时刻的速度和位移表达式中引入两个参数
时刻的速度和位移表达式中引入两个参数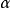 、
、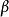 ,得纽马克法的两个基本方程:
,得纽马克法的两个基本方程:
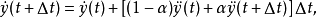
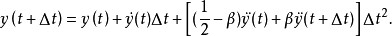
若在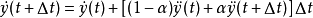 和
和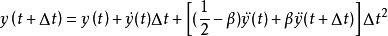 两个式子中令
两个式子中令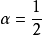 ,只保留参数
,只保留参数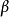 ,即为纽马克-
,即为纽马克-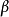 法。
法。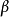 值常取为
值常取为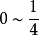 ;令
;令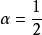 ,
,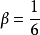 ,这就相当于加速度在
,这就相当于加速度在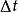 时段内线性变化,即威尔逊-
时段内线性变化,即威尔逊-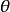 法中
法中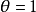 的情况;若令
的情况;若令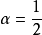 ,
,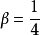 ,这相当于加速度在
,这相当于加速度在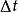 内为常量,其值为
内为常量,其值为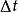 两端加速度的平均值,即为平均加速度法。
两端加速度的平均值,即为平均加速度法。
由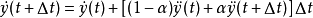 和
和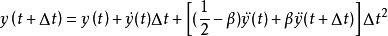 两个式子,可得:
两个式子,可得:
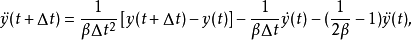
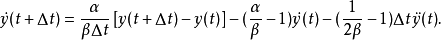
将上面两个式子代入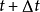 时刻的动力方程,经整理后得:
时刻的动力方程,经整理后得:
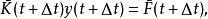 式中
式中
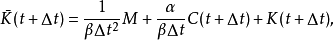
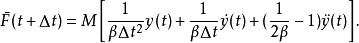
纽马克- 法的计算精度取决于时间步长
法的计算精度取决于时间步长 的大小。而时间步长的确定必须考虑荷载变化情况和系统自振周期的长短。为了保证感兴趣的高频分量的贡献,通常要求
的大小。而时间步长的确定必须考虑荷载变化情况和系统自振周期的长短。为了保证感兴趣的高频分量的贡献,通常要求 小于对响应有重要影响的最小结构自振周期的
小于对响应有重要影响的最小结构自振周期的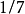 。稳定性研究还表明:当
。稳定性研究还表明:当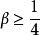 时,纽马克-
时,纽马克-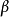 法是无条件稳定的;
法是无条件稳定的;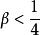 时,则是有条件稳定的,其稳定性条件为:对于
时,则是有条件稳定的,其稳定性条件为:对于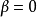 ,
,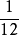 和
和 这三种情况,
这三种情况,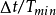 必须分别小于
必须分别小于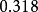 ,
,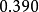 和
和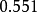 ,其中
,其中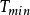 为结构的最小自振周期。2
为结构的最小自振周期。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

