如果存在一个观测器增益矩阵L使A -LC所有的特征值都具有严格的负实部，则线性状态方程[或者简单记为矩阵对(A，C)]是可检的。

已经知道，对于一个能观的状态方程，通过适当选择观测器增益矩阵任意配置观测器误差动态方程特征值来构造状态观测器。由配置这些特征值的自由度说明可以渐进稳定观测器误差动态方程，因此可以说能观性是通过观测器增益矩阵渐进稳定观测器误差动态方程的充分条件。在状态方程不能观的情况下，来研究观测器误差动态方程还是不是能渐进稳定的。因此引入了可检性的概念。将看到可检性和可镇定性之间也存在像能观性和能控性之间类似的对偶关系。首先介绍可镇定性的例子。状态方程如下：

其中矩阵对(Al1，C1)确定了一个能观一维子系统。根据观测器增益向量L=[Z．，Z。，l3]1，其中很容易选择观测器增益￡，来单独配置能观子系统的特征值。根据下三角矩阵块结构， A-LC的三个特征值为1+/1，和不能观子系统的特征值-1和-2。这样可以得出结 论，虽然状态方程是不能观的，仍然可能构造观测器增益向量确定一个观测器，得到由A- LC特征值确定的渐进稳定的状态观测器误差动态方程。需要强调的是，渐进稳定的观测 器误差动态方程可以直接得到，因为不能观子系统不受观测器增益向量的影响，从一开始就是渐进稳定的。也看到观测器增益Z。和Z。不对A-LC的特征值产生影响。1

如果存在一个观测器增益矩阵L使A -LC所有的特征值都具有严格的负实部，则线性状态方程(8.1)[或者简单记为矩阵对(A，C)]是可检的。
　　这个定义和先前的特征值配置结果看到，如果系统是能观的，那么就是可检的。另一方面，上述例子说明反之是不成立的。一个状态方程可以是能检的，但不一定是能控的，即可镇定性条件比能控性弱一样。
　　上述例子的分析可以推广如下：如果矩阵对(A，C)是能观的，那么它就是可检的，这个已经指出了，所以来看看矩阵对(A，C)不能观的情况。知道存在坐标变换x(t)一Tz(t)，使得变换后的状态方程为下图所示：

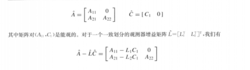
其特征值包括A11一L1C1的特征值和A22的特征值。因为(A11，Cl)是能观矩阵对，因此可以选择L1使A1l -L1C1的特征值具有严格的负实部。然而，A22不能观子系统不受观测器增益矩阵的影响，对于任意的L，A22的特征值都包括在A- LC的特征值中。因此，为了使A - LC的每一个特征值都具有严格的负实部，A22的特征值就必须具有严格的负实部。因此我们看到，当矩阵对(A，C)不能观时，可检性要求不能观子系统是渐进稳定的。我们也看到Lz在此分析中没有起到任何作用。
　　为了推导和前面可镇定性类似的可检性Popov-Belevitch-Hautus代数判据，我们首先建立与能控性和能观性关系类似的可镇定性和可检性之间的正式对偶关系。具体来讲，我们可以给出如下命题：矩阵对(A，B)是可镇定的，当且仅当矩阵对(Ar，Br)是可检的。矩阵对(A，C)是可检的，当且仅当矩阵对(AT，CT)是可镇定的。
　　对于第一句，如果矩阵对(A，B)是可镇定的，那么根据定义，存在状态反馈增益矩阵K，使A-BK的所有特征值都具有负实部。因为矩阵转置不影响特征值，因此(A—BK)T—AT_K7 BT的特征值也具有严格的负实部。将Kr看作是观测器增益矩阵，可知矩阵对(AT，BT)是可检的。将上述步骤颠倒，就可以建立逆命题，从而第二句可以用类似的方法讨论。

可镇定性Popov-Belevitch-Hautus判据根据对偶性，可得到可检性的判据为：

下列命题是等价的：

1．矩阵对(A，C)是可检的。

2．不存在A的非负实部特征值对应的右特征向量和C的所有行正交。

3．对所有具有非负实部的实数A，矩阵订兰页]具有满列秩。

证明：此定理可由下列的关系来证明：

矩阵对(A，C)是可检的，当且仅当矩阵对(Ar，CT)是可镇定的。

存在A的非负实部特征值对应的右特征向量和C的所有行正交，当且仅当存在Ar的非负实部特征值对应的左特征向量和CT的所有列正交。

如下图的题目：

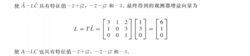
从例题中看到V3 =[2 3 1]T为A的特征值λ3=-3