贝特朗判别法是判断正项级数收敛与发散的一种方法。这是由贝特朗 (Bertrand,J.L.F.) 于 1842 年建立的。
简介贝特朗判别法是判断正项级数收敛与发散的一种方法。
设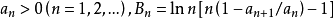 。若
。若 ,则级数
,则级数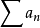 收敛;若
收敛;若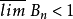 ,则
,则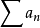 发散。
发散。
这是由贝特朗 (Bertrand,J.L.F.) 于 1842 年建立的。1
正项级数收敛性判别部分和数列判别法 正项级数的部分和数列
正项级数的部分和数列 是单调增加的数列即:
是单调增加的数列即: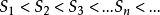 ,
, 收敛的充要条件是有界,因此有:
收敛的充要条件是有界,因此有:
正项级数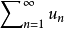 收敛的充要条件是:它的部分和数列
收敛的充要条件是:它的部分和数列 有界,即存在某正数
有界,即存在某正数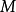 ,对于一切正整数
,对于一切正整数 有
有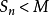 。
。
比较原则设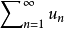 和
和 是两个正项级数,如果存在某正数
是两个正项级数,如果存在某正数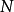 ,使得对一切
,使得对一切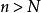 都有
都有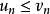 ,则有:
,则有:
(1)若级数 收敛,则级数
收敛,则级数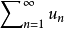 也收敛;
也收敛;
(2)若级数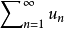 发散,则级数
发散,则级数 也发散。
也发散。
比式判别法(达朗贝尔判别法)设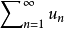 为正项级数,且存在某正常数
为正项级数,且存在某正常数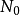 及常数
及常数 。
。
(1)若对一切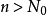 ,成立不等式
,成立不等式 ,则级数
,则级数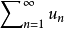 收敛;
收敛;
(2)若对一切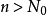 ,成立不等式
,成立不等式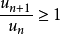 ,则级数
,则级数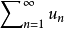 发散。
发散。
比式判别法的极限形式:
设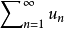 为正项级数,且
为正项级数,且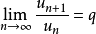 ,则有:
,则有:
(1)当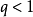 时,级数
时,级数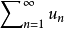 收敛;
收敛;
(2)当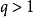 或
或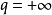 时,级数
时,级数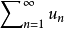 发散。
发散。
注意:若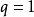 ,这时用比式判别法不能对级数的敛散性做出判别,因为它可能是收敛的,也可能是发散的,例如级数
,这时用比式判别法不能对级数的敛散性做出判别,因为它可能是收敛的,也可能是发散的,例如级数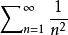 和
和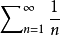 ,他们的比式极限都是
,他们的比式极限都是 ,但
,但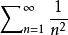 是收敛的,
是收敛的,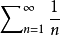 却是发散的。
却是发散的。
根式判别法(柯西判别法)设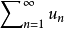 为正项级数,且存在某正常数
为正项级数,且存在某正常数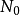 及正常数
及正常数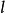 。
。
(1)若对一切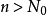 ,成立不等式
,成立不等式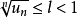 ,则级数
,则级数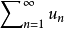 收敛;
收敛;
(2)若对一切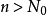 ,成立不等式
,成立不等式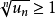 ,则级数
,则级数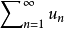 发散;
发散;
柯西判别法的极限形式:
设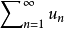 为正项级数,且
为正项级数,且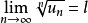 ,则:
,则:
(1)当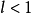 时,级数
时,级数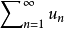 收敛;
收敛;
(2)当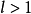 ,级数
,级数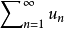 发散。
发散。
注意:若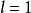 ,这时用根式判别法不能对级数的敛散性做出判别,因为它可能是收敛的,也可能是发散的,例如级数
,这时用根式判别法不能对级数的敛散性做出判别,因为它可能是收敛的,也可能是发散的,例如级数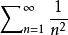 和
和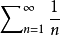 ,他们的比式极限都是
,他们的比式极限都是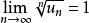 ,但
,但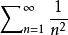 是收敛的,
是收敛的,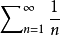 却是发散的。
却是发散的。
积分判别法积分判别法是利用非负函数的单调性和积分性质,并以反常积分为比较对象来判断正项级数的敛散性。
设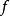 为
为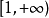 上非负减函数,那么正项级数
上非负减函数,那么正项级数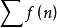 与反常积分
与反常积分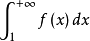 同时收敛或同时发散。
同时收敛或同时发散。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

