弦线支距法是测量曲线极为简易而精确的方法，适用于平坦无障碍物的区域。是一种根据切线支距法和偏角法的特点摸索出的方法。

概念弦线支距法是指以圆曲线的弦为X轴，弦的垂线为Y轴，以每段的起点为原点，计算曲线上各点的坐标值，在实地测设曲线的方法。

有如下特点：

（1）计算简便：曲线支距可在国标参考表中查出，或以计算尺按抛物线插入法求出。一切计算工作均可在现场立即进行。

（2）测设方法简便：安置仪器的站数较少，只瞄方向，不调角度，标明支距数后测量工作即可开展。测设曲线大多在定切线后返回仪器途中完成。

（3）容易检查，不易发生错误，精度高：曲线由两端向中间测设，支距由仪器瞄准，误差不累积等均使测设曲线精度大为提高，检查方法简单，有错误立即发现纠正。1

弦线支距法在地下工程施工测量中的应用探讨内容简介地下工程平面线型设计中，往往圆曲线和带有缓和曲线的圆曲线总长所占的比重比直线总长大。在许多地下工程隧道施工掘进过程中，测设曲线常用的方法有切线支距法、控线偏距法、弦线支距法，经过各种地下工程施工测量的长期实践，弦线支距法是测设曲线最适用而且运用范围有待于进一步推广的一种测没曲线的方法。2

曲线测量实例地下铁道和其它各种地下工程施工日益增多，曲线隧道在开挖过程中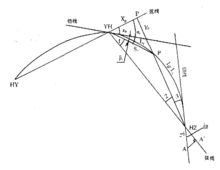需要随时提供方向线。为了在施工中满足施工工艺的要求和节约人力、物力等，采用激光指向仪指向，弦线支距法公式计算弦长和支距值，激光指向仪配合水平尺，结合弦长和支距值即可指导曲线隧道的测设和施工。

线支距法公式是在工程实践需要的基础上推导出来的，用PCI500机和BASIC语言编程或用CASIO、fx--4800P计算器编程来计算弦长和支距值，速度快且采用整套严密公式计算精度高。弦线支距法由于其适应面广，支距值精确且小，便于量距测设和施工，测设精度高、误差不积累等优点。在工程实践中正得到普遍重视和广泛应用，如北京地铁西东和东王区间，深圳地铁车竹区间，天东站一、二层联络通道和曲线出入口通道，以及曲线过街道和各类地下暗挖管线等。

实际工作中，根据曲线的设计情况和开挖竖井及掌子面的位置情况，灵活运用公式，并且注意公式中符号的意义，建立起整套的弦长和支距值内业资料，激光指向仪指出弦线的方向和坡度，根据弦长量出对应的支距值来定出曲线隧道架设钢格栅的中线点。弦线支距法公式思路明确并经工程实践验证，同样也适用于各种设计参数的山岭隧道曲线测设中。弥补和丰富了曲线隧道掘进过程中曲线测设方法的不足，有普遍的推广价值。

弦线支距法在曲线隧道施工测量中的应用曲线隧道测设方案的比选在线路测量中，曲线测量是比较复杂而又非常重要的一项工作，长期以来，测设曲线一直采用偏角法和切线支距法。其中偏角法较为普遍，优点是易校核，适用于山区及平原地区；缺点是误差积累。切线支距法方法简单，误差不积累；缺点是不能发现中间点的测量错误，仅适用于平坦地区。

提出一种新的曲线测设方法——弦线支距法。如图1，把曲线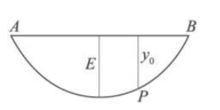A、B之间的两个端点用直线连接起来，以弦线AB为基准计算支距。不难看出，AB两点支距都为0；曲线向前延伸，曲线上任一点P点的支距y0将逐渐变大，大到一个极大值E为止再变小，最终为0，则支距y0值始终在一个有上限值的范围内变化。即弦线支距法以曲线的两个端点连接而成的弦线为基准线，通过量取基准线上任一点支距(垂线)y0，即可定出曲线。该方法简单方便，且在激光向仪的配合下，放样数据十分精确。

弦线支距法的原理以圆曲线为例，说明弦线支距法的原理。如图2所示，根据等腰三角形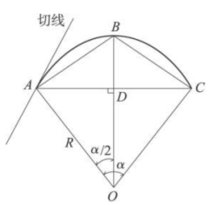的角分线垂直平分对边的几何原理，利用三角函数关系，即可求任一点的支距值。假设以AC弦线为X轴，DB为y轴，实际测设中，把仪器支于A点，沿弦线方向量取xp定出D点，于D点定出AC线的垂分线，在垂分线(y轴)上量取yp即可定出圆弧上B点，依次类推测出其他点。

测设要点在工程曲线所占比例较大时，在开挖过程中用激光指向仪安置于弦线方向，根据计算好的各点量取对应弦长和支距值，指导曲线隧道架立钢格栅、喷锚、衬砌、开挖等施工工艺。实践表明，该方法具有支距短、误差不积累、简单、弦线和激光指向仪变动次数少等优点，为暗挖隧道按时贯通争取了时间，贯通误差均小于规范允许的限差，值得在同类工程中推广。3

本词条内容贡献者为:

陈红 - 副教授 - 西南大学