在拉丁方设计中，三个因素要求相同的水平数，即行，列，字母数均相同，但在具体实践中可能其中一个因素水平数较少，这时就不能采用完整的拉丁方设计，则可用不完全拉丁方设计(Incomplete Latin Squares)，也称YOUDEN SQUARES。这种设计由于类似于随机区组设计中平衡不完全区组设计，形式上是一种不完善的拉丁方，故称不完全拉丁方设计。

基本介绍不完全拉丁方设计类似于平衡不完全随机区组设计，在3因素的拉丁方设计中，当处理水平数固定的情况下，如果其他两个区组因素中有一个水平数小于处理水平数，此时不满足拉丁方设计中水平数必须相等的条件，可以考虑采用不完全拉丁方设计。不完全拉丁方设计虽然称为Youden square，但它实际上已经不是square了，因为行列数并不相等。不完全拉丁方设计亦称尤登方设计，是用尤登方安排的一种部分实施试验设计。用于由于客观条件的限制无法完整地用拉丁方安排试验的情形，或者用于由拉丁方设计的试验结果有丢失数据的情形，其结果的分析与拉厂方设计类似。

通常所说的不完全拉丁方设计（也称“尧敦方设计”）的形式是列区组的水平数k小于行区组水平数b(等同于处理水平数t)的设计，该设计共bc个受试对象。如果仅看列区组，不考虑行区组，尧敦方设计是一个完全随机区组设计；如果仅看行区组，不考虑列区组，尧敦方设计则是一个平衡不完全随机区组设计，图1给出了3×2、4×3两种不完全拉丁方设计的形式1。

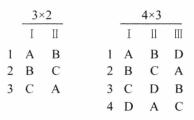
图1是不完整拉丁方设计的一个样式例子。这是一个具有7种水平，7行3列的设计，重要的是将不同水平被分配到行列的顺序，注意除具有平衡不完全区组设计的特点外，YOUDEN方设计中，每一种处理在每列中恰好出现一次。处理数t等于区组数b。

|| || 表1

YOUDEN方设计有些可以通过平衡不完全设计得到，有些可以通过设计完全拉丁方法后略去某一行或列而获得。

YOUDEN方设计用于处理因素水平数较多的实验，有多种类型的处理因素。由于列数少于处理数，所以每一行仅有部分处理方式被应用。有时一些双向控制变量或双向分类的实验需要这种设计2。

应用条件当客观条件限制不能用拉丁方设计时，可用拉丁方的一部分来安排试验，称为不完全拉丁方(或Youden方、尧敦方)设计。或虽用了拉丁方设计，但某一行或某一列缺失数据较多，又无法补救时，可根据情况作不完全拉丁方资料处理。

不完全拉丁方设计的特点不完全拉丁方设计的主要特点为：

(1)处理水平数t等同于行数b，处理水平重复数r等同于列数k。处理水平每列出现1次，每行最多出现1次。

(2)每一对处理在行区组中出现的次数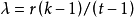，是一自然数。如3×2尧敦方设计中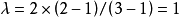，，每一对处理(AB、AC、BC)在行区组中各出现1次；4×3尧敦方设计中，，每一对处理(AB、AC、AD、,BC、BD、CD)在行区组中各出现2次1。

本词条内容贡献者为:

刘军 - 副研究员 - 中国科学院工程热物理研究所