道奇-罗米格表是由美国的道奇(H.F.Dodge)和罗米格(H.G.Romig)在20年代所创的一套对批量产品进行计数抽样的计划表,曾广泛用于工业方面的抽样检验。这套表共分二类:一类是建立在批容许不合格率(LTPD)基础上,另一类是建立在检后平均不合格率上限(AOQL)基础上。每一类又分为一次抽样和二次抽样二种表,因此一共有四套不同的抽样表。每套表又有控制在不同水平的表。这个表的优点是在给定一种检验方法后可以查出抽验最小的次数1。
基本介绍在1944年,道奇和罗米格发表了一本关于计数抽样表和计数抽样方法的著作,书名为《抽样检查表》;1959年出版了修订的第二版。道奇—罗米格的抽样检查方案是准备在贝尔电话公司应用的,目的在于减少总检查量,假定每批拒收的产品经过筛选。两种应用依据——批容许不合格品率(LTPD)和平均检出质量界限(AOQL)——都有一次抽样检查表和二次抽样检查表,一共有四类可用方案2。
LTPD的一次或二次抽样检查表注有8个LTPD值(0.005,0.01,0.02,0.03,0.04,0.05,0.07和0.10)。使用方风险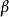 定为0.10。表格为不同批量和质量平均值规定了样本大小和接收数。对任何给定的批量,有六种方案可供选择,各自用于不同的工序平均值。如果所选的方案符合实际的工序平均不合格品率,这种方案就能保证其平均检查量小于共他五种方案。
定为0.10。表格为不同批量和质量平均值规定了样本大小和接收数。对任何给定的批量,有六种方案可供选择,各自用于不同的工序平均值。如果所选的方案符合实际的工序平均不合格品率,这种方案就能保证其平均检查量小于共他五种方案。
AOQL一次和二次抽样检查表附注的AOQL值如下:0.001,0.0025,0.005, 0.0075, 0.01, 0.015, 0.02, 0.025, 0.03, 0.04,0.05, 0.07, 0.10。
表格给出各种方案的批容许不合格品率。这些方案同样具有这种特性,即对符合实际工序平均不合格品率的方案,其平均检查量最小2。
道奇-罗米格抽检表的分类道奇-罗米格抽检表分为四类:
(1)规定极限不合格率LTPD的单次抽样方案;
(2)规定极限不合格率LTPD的双次抽样方案;
(3)规定平均出厂极限不合格率AOQL的单次抽样方案;
(4)规定平均出厂极限不合格率AOQL的双次抽样方案。
关于挑选检验挑选检验(rectifying inspection)是对验收抽样所拒收的批的全部产品或规定量产品进行检查,以剔出或替换其中不合格品的检验。是一种特殊的计数抽样检验。有道奇-****罗米格挑选检验和安斯库姆挑选检验。
道奇-罗米格挑选检验道奇-罗米格挑选检验是参考道奇-罗米格表和历史资料,在保证检验中批允许不合格品率(LTPD)或平均检出质量上限(AOQL),并使平均检验总数(ATI)最少的一种挑选检验。首先分别找LTPD或AOQL查表,按批量n和过程平均来选择ATI最小的检验方案。如果不知道过程平均,则用表中最大值确定采用一或二次抽样和相应接收判据,检验出不合格批进行100%检验,以剔出或更换不合格品。道奇-罗米格的检验表于1944年出版。这一方法主要用于企业内部非破坏性检验,也用于外贸产品检查。在批量非常大时,用这种检验方法较难处理。
安斯库姆挑选检验安斯库姆挑选检验是1949年提出的。与道奇-罗米格法不同之处,是对不合格批不靠100%检验,而是继续抽验下去,直到满足停验规则,而且被接收或把产品验完并以合格品替换不合格品为止。停验规则应使质量坏的批抽验多些,质量好的批抽得少些,保证LTPD又使ATI最小。方法是利用安斯库姆表,以LTPD=p,估计 ,已知批量N,p=0.1,查表
,已知批量N,p=0.1,查表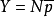 ,由表查ASN/N(带星号)乘N,得ASN,ASN=ATI为最小;用表中同一排
,由表查ASN/N(带星号)乘N,得ASN,ASN=ATI为最小;用表中同一排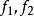 分别乘批量N得到第一和第二样本的样本量
分别乘批量N得到第一和第二样本的样本量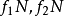 ,由表查得AOQL(即(N)AOQL),
,由表查得AOQL(即(N)AOQL),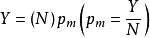 。接收判据:第一样本没出现不合格品,第一和第二样本累计不超过一个不合格品,第一至第i样本累计不超过i-1个不合格品,则验收3。
。接收判据:第一样本没出现不合格品,第一和第二样本累计不超过一个不合格品,第一至第i样本累计不超过i-1个不合格品,则验收3。
与其它表的比较挑选型抽样,最早是美国贝尔电话研究所的道奇和罗米格两人提出来的,他们设计的抽检表称为道奇-罗米格表,至今还得到广泛的应用。日本人在道奇-罗米格抽检表的基础上制定了日本挑选型抽样标准JISZ9006。这两类抽检表大同小异,都可供参考使用。它们共同的特点是:
①都对AOQL和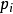 划分了级别,形成了系列;
划分了级别,形成了系列;
②都对过程平均不合格率 划分了级别,形成了系列;
划分了级别,形成了系列;
③都对批量N划分了级别。这两类方案具体的级别划分及相互的异同点如表1所
表1
|| ||
GB/T 13546与道奇-罗米格表和JIS Z 9006的主要区别
GB/T 13546与道奇-罗米格表和JIS Z 9006有如下区别:
a.GB/T 13546中的LQ值和AOQL值系列均采用优先数系,而后两篇文献中则不然;
b.GB/T 13546中的 值范围的上限也采用优先数系,而后两篇文献中则不然;
值范围的上限也采用优先数系,而后两篇文献中则不然;
c.GB/T13546中批量范围的划分与国家标准GB 2828和ISO2859-1基本上一致,而后两者则不然;
d.当批量N≤500时,GB/T 13546中凡涉及累计超几何概率计算时均采用精确计算,只当N>500时使用莫伦纳尔近似式;而后两篇文献中,不管批量大小如何,基本上都采用其他一些近似计算,误差较大4。
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

