在量子力学中，克莱布希－高登系数（Clebsch–Gordan

coefficients，简称 CG 系数，又称向量耦合系数等）是两个角动量耦合时，它们的本征函数的组合系数。从数学的角度，克莱布希－高登系数出现在紧李群的表示论中，它研究的是两个不可约表示的张量积如何分解成不可约表示的直和。克莱布希－高登系数因阿尔弗雷德·克莱布什和保罗·哥尔丹而得名。

定义从角动量的一般量子理论出发，以角动量算符的对易关系为基础，不涉及角动量算符在某个具体表象下的表示。给定了j之后，本征函数组1

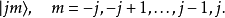张开成一个 2j+1 维的函数空间。

现在给定两个量子数j1和j2，则其本征函数组张开的空间分别有 2j1+1 维 与 2j2+1 维。现考虑这两个函数空间的张量积：

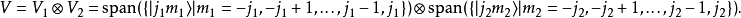
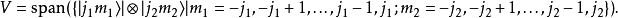
下面为简便起见，定义新的记号

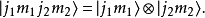一般地，若f,g分别是这两个空间里的算符，则在积空间上可以定义下列算符：

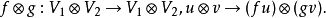另一方面，定义在这两个空间上的算符可以自然地嵌入到积空间中，只需取

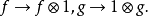其中 1 表示恒等操作（算符）。

在这样的定义下，两个角动量算符的的耦合表达为：

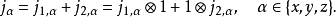
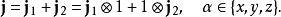容易验证这样定义的j满足角动量的基本对易关系，因此是一个角动量算符，称为总角动量算符。

根据角动量的一般理论，总角动量算符也有自己的本征函数组，它可以用积空间里的基来表示

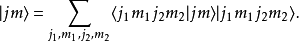这里的线性组合系数

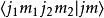就被称为克莱布希－高登系数。在正交归一性的要求下，克莱布希－高登系数仍然具有相位不确定性。本文中取 Condon-Shortle 惯例，使所有克莱布希－高登系数为实数。

例子以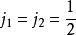 为例。

对任意一个算符 f，本节中的矩阵元表示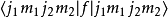 的值。

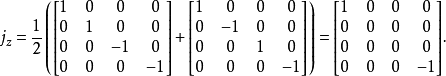
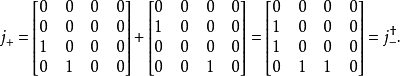
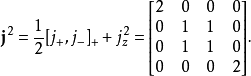
计算最后一个矩阵的本征值和本征向量，得到

于是可到克莱布希－高登系数。从上面的例子可以看到，对于一般的情况，用矩阵来求克莱布希－高登系数将是十分繁琐的。一般可以采用下面的 Racah 表达式计算，更多的情况是直接查表。

Racah 表达式Racah 用代数方法得出了克莱布希－高登系数的有限级数表达式。2

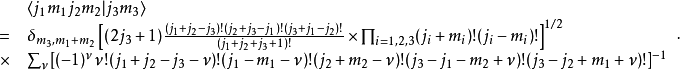其中，ν的求和限制在使得所有的阶乘因子中的数非负的范围内。

对称性克莱布希－高登系数有下列的对称性

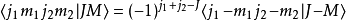
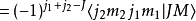
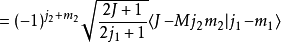
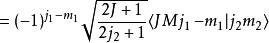
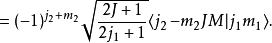
其他关系克莱布希－高登系数与维格纳 3-j符号有下列关系：

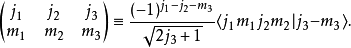后者可以用于计算下列形式的球谐函数积分：

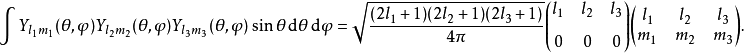由球谐函数的正交归一性，上面的结果也可以用来对球谐函数作展开。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所