在量子力学里,相互作用绘景(interaction picture),是在薛定谔绘景与海森堡绘景之间的一种表述,为纪念物理学者保罗·狄拉克而又命名为狄拉克绘景。在这绘景里,描述量子系统的态矢量与表达可观察量的算符都会随着时间流易而演化。有些实际案例会涉及到因相互作用而使得量子态与可观察量发生改变,这类案例通常会使用狄拉克绘景。1
定义为了便利分析,位于下标的符号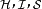 分别标记海森堡绘景、狄拉克绘景、薛定谔绘景。通过对于基底的一种幺正变换,算符和态矢量在狄拉克绘景里的形式与在薛定谔绘景里的形式相关联。
分别标记海森堡绘景、狄拉克绘景、薛定谔绘景。通过对于基底的一种幺正变换,算符和态矢量在狄拉克绘景里的形式与在薛定谔绘景里的形式相关联。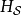 在量子力学里,对于大多数案例的哈密顿量,通常无法找到薛定谔方程的精确解,只有少数案例可以找到精确解。因此,为了要能够解析其它没有精确解的案例,必须将薛定谔绘景里的哈密顿量分成两个部分,2
在量子力学里,对于大多数案例的哈密顿量,通常无法找到薛定谔方程的精确解,只有少数案例可以找到精确解。因此,为了要能够解析其它没有精确解的案例,必须将薛定谔绘景里的哈密顿量分成两个部分,2
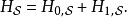 其中,
其中,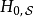 有精确解,有广泛知悉的物理行为,而
有精确解,有广泛知悉的物理行为,而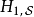 则通常没有精确解,是对于系统的摄动。
则通常没有精确解,是对于系统的摄动。
假若哈密顿量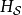 含时(例如,感受到时变外电场作用的量子系统,其哈密顿量会含时),则通常会将显性含时部分放在
含时(例如,感受到时变外电场作用的量子系统,其哈密顿量会含时),则通常会将显性含时部分放在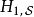 里。这样,
里。这样,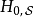 不含时,而时间演化算符U(t)的公式可以简单地表示为
不含时,而时间演化算符U(t)的公式可以简单地表示为
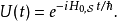 其中,t是时间。
其中,t是时间。
假若对于某些案例,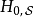 应该设定为含时,则时间演化算符的公式会变得较为复杂:
应该设定为含时,则时间演化算符的公式会变得较为复杂:
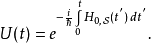 本条目以下内容假设
本条目以下内容假设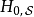 不含时。
不含时。
态矢量在狄拉克绘景里,态矢量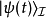 定义为
定义为
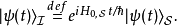 其中,
其中, 是在薛定谔绘景里的态矢量。
是在薛定谔绘景里的态矢量。
由于在薛定谔绘景里, 态矢量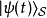 与时间的关系为
与时间的关系为
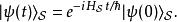 所以,在
所以,在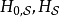 对易的条件下,可以有
对易的条件下,可以有
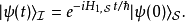
算符在狄拉克绘景里的算符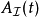 定义为
定义为
 其中,
其中,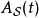 是在薛定谔绘景里对应的算符。
是在薛定谔绘景里对应的算符。
时间演化方程以下内容,算符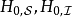 都简略标记为
都简略标记为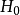 。
。
量子态从态矢量的定义式,可以得到态矢量对于时间的导数是
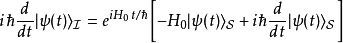
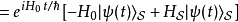
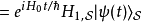
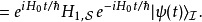 将算符的定义式代入,可以得到
将算符的定义式代入,可以得到
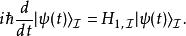 这是施温格-朝永振一郎方程的一个较为简单的形式。
这是施温格-朝永振一郎方程的一个较为简单的形式。
算符假若算符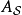 不含时,则其对应的
不含时,则其对应的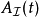 的时间演化为
的时间演化为
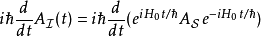
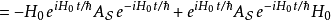
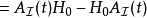
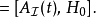
这与在海森堡绘景里,算符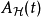 的时间演化类似:
的时间演化类似:
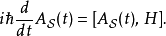
密度矩阵应用施温格-朝永振一郎方程于密度矩阵,则可得到
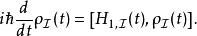
各种绘景比较各种绘景随着时间流易会呈现出不同的演化:3
|| ||
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

