在数理逻辑中，直觉主义逻辑的布劳威尔-海廷-柯尔莫哥洛夫释义或BHK释义是由鲁伊兹·布劳威尔、阿兰德·海廷和独立的由安德雷·柯尔莫哥洛夫提出的。它有时也叫做可实现性释义，因为有关于斯蒂芬·科尔·克莱尼的可实现性理论。

释义释义精确的陈述一个给定的公式的证明是什么。这是通过这个公式的在结构上归纳规定的：

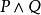的证明是有序对，这里的a是P的一个证明而b是Q的一个证明。

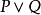的证明是有序对，这里的a是0而b是P的证明，或者a是1而b是Q的证明。

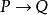的证明是函数f: P→Q，它把P的证明变换成Q的证明。

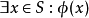的证明是有序对，这里的a是S的一个元素，而b是φ(a)的一个证明。

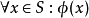的证明是函数f: a→φ(a)，它把S的一个元素a变换成φ(a)的证明。

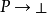的证明被定义为 ，它的证明是把P的证明变换成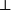的证明的一个函数。

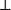是荒谬。应当没有它的证明。

假定从上下文获知原始命题的释义。

荒谬与函数逻辑系统不可能有形式否定算子，使得在没有P的证明的时候有正确的 非P的证明（参见哥德尔不完备定理）。BHK释义转而采纳 非P为意味着P导致荒谬，指示为，所以¬P的证明是把P的证明变换成荒谬的证明的函数。

荒谬的标准例子可以在算术中找到。假定0=1，并进行数学归纳法：0=0通过等同公理得到；（归纳假设）如果0等于特定自然数n，则1将等于n+1 (皮亚诺公理：Sm = Sn当且仅当m = n)，但是因为0=1，所以0也等于n+1；通过归纳，0等于任何数，所以任何两个自然数都是相等的。

所以，有从0=1的证明得到任何基本算数等式和进而任何复杂算术命题的一种方式。进一步的说，要得到这种结果，不是必须的涉及皮亚诺公理0不是任何自然数的后继。这使得0=1在Heyting算术（皮亚诺公理被重写0=Sn → 0=S0）适合充当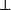 。这种0=1的使用验证了爆炸原理。

BHK释义依赖于制定把一个证明变换成另一个证明，或者把一个域的元素变换成一个证明的函数的观点。不同版本的数学构造主义在这一点上是有分歧的。

Kleene的可实现性理论把这种函数看成是可计算函数。它处理Heyting算术，这里的量化的域是自然数而原始命题有x=y的形式。x=y的证明简单是平凡的算法，如果x求值得到与y求值同样的数（它对于自然数总是可决定的），否则没有证明。可以通过归纳建造起更复杂的算法。

可实现性可实现性是可用来处理关于公式的信息而不是关于公式的证明的那部分证明论。自然数n被称为实现了自然数算术的语言中一个陈述。其他逻辑和数学陈述也是可实现的，假如提供了解释合式公式一种方法，而不用借助达成这些公式的证明。

斯蒂芬·科尔·克莱尼在1945年介入了可实现性的概念，寄希望于它成为直觉逻辑推理的忠实典范，但这个设想最初由Rose反证了一个可实现的命题公式的例子，它在直觉演算中是不可证明的。可实现性似乎由于它的复杂度而难于公理化，但它可以通过高阶Heyting算术（HA）来达成。

改进可实现性使用有类型lambda演算作为语言实现者。改进可实现性是展示马尔科夫原理在直觉逻辑中不可推导的一种方式。正相反，它允许构造性的证实前提的独立性原理： 。

相对可实现性是非必需可计算的数据结构的递归或递归可枚举元素的直觉主义分析，比如在实数在数字计算机系统上只能近似表示的时候在所有实数上的可计算的运算。在计算机科学应用：改进可实现性证实了实施于某些证明辅助工具比如Coq中的“证明提取”过程。

直觉类型论与直觉主义逻辑经典逻辑是理想主义的，纯教条的。构造逻辑是现实主义的，它给数学公式经验的内容。直觉主义逻辑更多地从证明论和模型论的角度展现逻辑：也就是说，它是一个构造的逻辑。所谓构造性是指：与经典逻辑只关心公式的真值不同，构造逻辑关注的是实际的证明对象本身。但是什么是构造呢?“构造”可以指一个过程以及执行该过程的结果1。

直觉类型论、或构造类型论、或Martin-Löf 类型论、或就叫类型论是基于数学构造主义的函数式编程语言、逻辑和集合论。直觉类型论由瑞典数学家和哲学家 Per Martin-Löf 在1972年介入。 Martin-Löf 已经多次修改了它的提议；先是非直谓性的而后是直谓性的，先是外延的而后是内涵的类型论变体。直觉类型论基于的是命题和类型的同一: 一个命题同一于它的证明的类型。这种同一通常叫做Curry-Howard同构，它最初公式化了命题逻辑和简单类型 lambda 演算。类型论通过介入包含着值的依赖类型把这种同一扩展到谓词逻辑。类型论内在化了 Brouwer、Heyting 和 Kolmogorov 提议的叫做 BHK释义的直觉逻辑释义。类型论的类型扮演了类似于集合在集合论的角色，但是在类型论中的函数总是可计算的。

直觉主义逻辑或构造性逻辑是最初由阿兰德·海廷开发的为鲁伊兹·布劳威尔的数学直觉主义计划提供形式基础的符号逻辑。这个系统保持跨越生成导出命题的变换的证实性而不是真理性。从实用的观点，也有使用直觉逻辑的强烈动机，因为它有存在性质，这使它还适合其他形式的数学构造主义。直觉逻辑的公式的语法类似于命题逻辑或一阶逻辑。但是直觉逻辑的连结词不像经典逻辑那样是可互定义的，因此它们的选择是重要的。在直觉命题逻辑中通常使用 →, ∧, ∨, ⊥ 作为基本连结词，把 ¬ 作为 ¬A = (A → ⊥) 的简写处理。在直觉一阶逻辑中量词 ∃, ∀ 都是需要的。不同在于很多经典逻辑的重言式在直觉逻辑中不再是可证明的。例子不只包括排中律 P ∨ ¬P，还有皮尔士定律 ((P → Q) → P) → P，甚至还有双重否定除去。在经典逻辑中，P → ¬¬P 和 ¬¬P → P 二者都是定理。在直觉逻辑中，只有前者是定理: 双重否定可以介入但不能除去。对很多经典有效重言式不是直觉逻辑的定理的观察导致了弱化经典逻辑的证明论的想法。

示例恒等函数是公式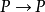的证明，不管P是什么。

无矛盾律被展开为：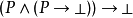

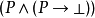的证明是函数f，它把 的证明变换成 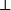的证明。

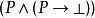的证明是证明的有序对，这里的a是P的证明，而b是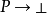的证明。

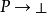的证明是把P的证明变换成的证明的函数。

把它们放置到一起，的证明是函数f，它把有序对变换成的证明 -- 这里的a是P的证明，而b是把P的证明变换成 的证明的一个函数。函数 证明了无矛盾律，不管P是什么。在另一方面，排中律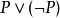展开为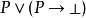，而一般没有证明。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学