对空间曲线而言，空间曲线在某点的单位切向量和副法向量所张成的平面为空间曲线的从切平面。对研究空间曲线的性质有着重要意义。

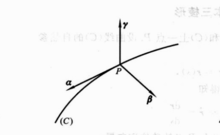
一、从切平面定义

给出 类空间曲线（C）和（C)上一点P，设曲线的（C）的自然参数表示为1：

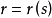
其中s是自然参数，定义：

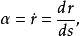
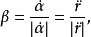
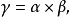
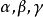分别为曲线上P点的单位切向量，主法向量和副法向量。P点上的三个向量构成右手系。

则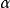 和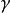 所确定的平面是曲线（C）上P点的从切平面。

二、从切平面方程1、自然参数方程

如定义，从切平面方程为：

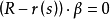
或

2、一般参数方程

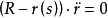
给定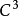 类空间曲线（C）2

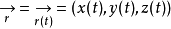
则曲线C在一点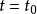 处的从切平面为：

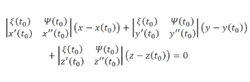
其中

三、计算实例

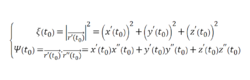
1、求曲线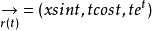 在原点的从切平面：

解:

,

,

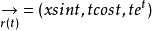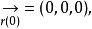
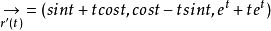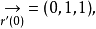
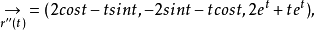
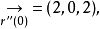
ξ(0)=2,Ψ(0)=2

所以，从切平面方程为

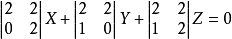
即

四、性质及意义

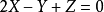
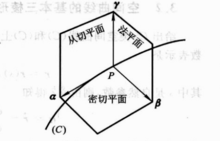
1、从切平面，法平面，密切平面所构成的图形称为曲线的基本三棱形。


　　

2、曲线r(s)的密切球面与从切平面的交线圆的圆心轨迹方程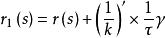

其中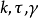分别为曲线的曲率，扰率和副法向量。

3、两条曲线的对应点的从切平面重合，则这两条曲线为达布曲线。3

本词条内容贡献者为:

朱坤平 - 副教授 - 华东理工大学