因子自由度（Factor degree of freedom）在统计数据中指统计量在最终计算中可随意变化的数值。自由度的数量定义为可完全指定系统位置的独立坐标的最小值。在数学上，自由度是随机向量域的维数，或者基本上是“自由”分量的数量。该术语最常用于线性模型（线性回归、方差分析）背景下，在某些随机向量被约束在线性子空间中，自由度数量是子空间的维数。

简介在统计数据中，因子自由度是统计量最终计算中可以随意变化的数值。动态系统可以移动的独立方式的数量不会违反强加给它的任何约束，称为自由度。换句话说，自由度的数量可以定义为可以完全指定系统位置的独立坐标的最小数量1。统计参数的估计可以基于不同量的信息或数，进入参数估计的独立信息的数量称为自由度。

在数学上，自由度是随机向量的域的维数，或者基本上是“自由”分量的数量（在完全确定向量之前需要知道多少组件）。

该术语最常用于线性模型（线性回归、方差分析）的背景下，其中某些随机向量被约束在线性子空间中，并且自由度的数量是子空间的维数。自由度通常还与这些矢量的平方长度（或坐标的“平方和”）以及在相关统计测试问题中出现的卡方分布或其他分布参数相关联。

虽然介绍性教科书可能会将因子自由度作为分布参数或通过假设检验引入，它是定义自由度的基础几何，对于正确理解这一概念至关重要2。

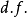符号在等式中，自由度的典型符号是 。在文本和表格中，通常使用缩写“ ”。RA Fisher曾用 表示自由度，但现在通常用 表示样本量

随机向量在几何学上，因子自由度可以解释为某些向量子空间的维数。作为一个起点，假设我们有一个独立正态分布观测样本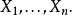： 这可以表示为一个 维随机向量：

由于这个随机向量可以位于维空间的任何地方，因此它具有个自由度。

现在，让我们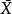 是样本的意思。随机向量可以分解为样本均值加残差向量之和：

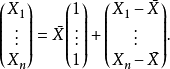
右侧的第一个向量被限制为1的向量的倍数，并且唯一的自由量是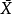 。因此它有1个自由度。

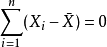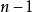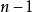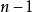第二个向量受关系限制 。这个矢量的第一个 分量可以任意选择。但是，一旦知道了前 个组件，该约束就会告诉您第 个组件的值。因此，这个矢量具有 个自由度。

在数学上，第一个向量是数据向量在1自由度的向量跨越子空间上的正交或最小二乘投影。1自由度是这个子空间的维度。第二个残差向量是该子空间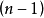 维正交补数上的最小二乘投影，具有 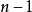个自由度。

在统计测试应用中，通常一个人对组件向量没有直接感兴趣，而是对它们的平方长度感兴趣。在上面的例子中，残差平方和是

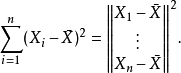
如果数据点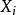以均值0和方差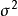分布 ，那么剩余的平方和具有缩放的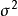卡方分布（按因子缩放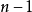），个自由度。因子自由度（这里是分布的参数）仍然可以被解释为底层矢量子空间的维度。

同样，单样本t检验统计量，

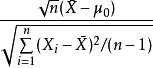
当假设均值时，遵循学生t分布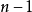，自由度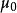是正确的。同样，自由度来自分母中的残差向量。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所