重数,数学名词,包括几何重数和代数重数。在矩阵运算中,该矩阵有特征值是重根,则该特征值所对应的特征向量所构成空间的维数,称为几何重数。(举例:一条直线与一个圆相切,那么切点的几何重数就是二,如果三条直线相交在一点,那么交点的几何重数就是三)
几何重数定义设矩阵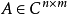 有
有 个个相异的特征值
个个相异的特征值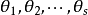 ,
, 的特征多项式
的特征多项式
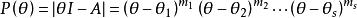 其中
其中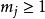 ,
,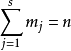 。
。
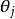 的代数重数是指,
的代数重数是指,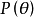 中
中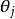 的重数
的重数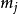 ;几何重数是指
;几何重数是指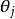 的的特征子空间
的的特征子空间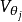 的维数
的维数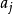 。
。
从 的
的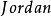 标准型
标准型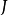 容易看出:
容易看出:
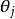 的代数重数
的代数重数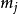 ,是
,是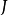 中以
中以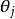 为主对角线元素的各
为主对角线元素的各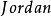 子块的阶数之和;
子块的阶数之和;
几何重数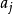 是
是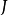 中以
中以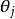 为主对角线元素的
为主对角线元素的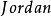 子块的个数1。
子块的个数1。
相关定理复方阵A可对角化的充分必要条件是A的每个特征值的几何重数与代数重数相等。
复方阵A的每个特征值对应的几何重数小于等于代数重数2。
代数重数指方程的根的重数,也就是说,方程的根是几重根。(举例:(x-2)3=0,这个方程的根为x=2,这个根是3重的,因此x=2的代数重数为3)
关系恒有此关系: 几何重数 ≤ 代数重数
本词条内容贡献者为:
刘军 - 副研究员 - 中国科学院工程热物理研究所


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

