若尔当标准型是由若干个主对角线为特征值，下方（或上方）次对角线全为1，其余全为0的若尔当块按对角排列组成的准对角矩阵。不是每个n阶矩阵通过初等变换都能化为对角矩阵，但每个n阶复数矩阵A通过初等变换都能化为若尔当标准型，这个若尔当形矩阵除去其中若尔当块的排列次序不同外是被矩阵A唯一确定的，它称为矩阵A的若尔当标准型。

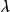定义若尔当块形式为的矩阵称为若尔当块（其中为复数）。即若当块矩阵对角线上为相同的复数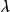，下方（或上方）次对角线上全为1，其余元素全为0。

若尔当标准型由若干个若尔当块组成的准对角矩阵称为若尔当标准型，其一般形状为，其中，并且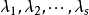中有一些可以相等。1

实例若尔当块实例例如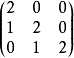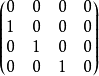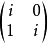，，都是若尔当块。

若尔当标准型实例例如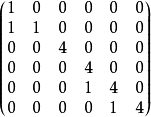是一个若尔当标准型矩阵。其由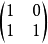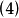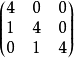，，等三个若尔当块组成。

理论推导与例子一般采用初等因子理论来完成若尔当标准型的理论推导，其具体推导过程参见王萼芳《高等代数》346-349页。1这里我们采用一个具体的例子来说明若尔当标准型的计算过程。

例：求矩阵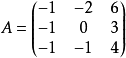的若尔当标准型。

解：首先求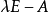的初等因子：

。

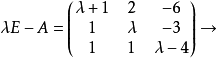
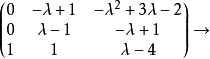
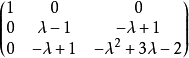
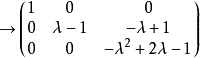
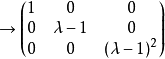因此，A的初等因子是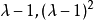，A的若尔当标准型是

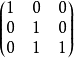
本词条内容贡献者为:

朱坤平 - 副教授 - 华东理工大学