萨蒙定理(Salmon theorem)又称沙尔蒙定理，是关于点共线和距离成比例的两个定理：1.自圆上一点引三弦．则以此三弦为直径的圆的其它三个交点共线；2.圆心O至A、B两点的距离，与A至B的极线及B至A的极线的距离成比例。该定理为英国数学家G.Salmon所发现，萨蒙(George Salmon，1819-1904)是英国数学家1。

基本介绍萨蒙(Salmon, 1819-1904年)是英国数学家。初期从事综合几何研究，后研究代数形式的不变量与共变量理论在曲线、曲面几何中的应用。先后写出几十篇论文和四本重要的教科书《圆锥曲线》、《高阶平面曲线》、《三维解析几何》等，在西欧各国出版，广泛流传，影响较大。萨蒙在数学上的其它贡献还有：三次曲面上的27条直线的发现；限定条件下的曲面性质；代数方程重根的条件等。

萨蒙定理是关于点共线和距离成比例的两个定理：

1.自圆上一点引三弦，并以它们各为直径画圆，则所画三圆的两两相交的三个与A不同的交点共线(如图)。

2.圆心O至A，B两点的距离与A至B的极线b的距离及B至A的极线a的距离成比例。

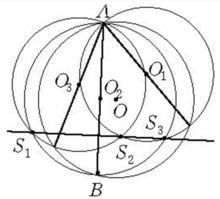
点共线及其证明从圆上任意一点引三条弦，并分别以这三条弦为直径作圆，则所作三圆的其它三个交点共线。

证明 设P为圆O上任一点，PA、PB、PC是任意作的弦，分别以PA、PB、PC为直径作圆OA、OB、OC，其中⊙OB与⊙OC、⊙OC与⊙OA、⊙OA与⊙OB的另一交点分别为D、E、F。

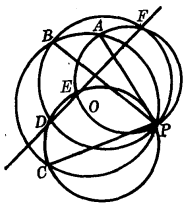
首先连接DB、DC，在⊙OB与⊙OC中，

∵ PB、 PC为直径，

∴∠PDB=∠PDC= 90°，

证得B、D、C三点共线，也即PD⊥BC于D。

同法可证PE⊥CA于E，PF⊥AB于F。

又P、A、B、C四点本来共圆，因此问题成为自△ABC外接圆上任-一点P作PD⊥BC、PE⊥CA、PF⊥AB垂足分别为D、E、F，要证D、B、F三点共线。而这就是西摩松线，所以本命题成立2。

距离成比例及其证明圆心O到A、B两点的距离与A到B的极线b及B到A的极线a的距离成比例。

该定理为英国数学家G.Salmon所发现，它是极和极线理论中的一个基本定理。

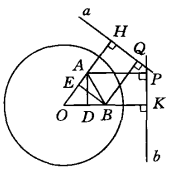
如图3，直线a、b分别是点A、B的极线，OA⊥a于H，OB⊥b于K，AP是A到极线b的距离，BQ是B到极线a的距离。作AD⊥OB于D，BE⊥OA于E，则A、E、D、B四点共圆，于是有

OD·OB=OE·OA， ①

又 OB·OK=R²=OA·OH，②

②一①得 OB(OK－OD)=OA(OH－OE)，

即 OB·AP=OA·BQ，

OA∶OB=AP∶BQ3。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所