超导体在磁场中的稳定结构中，其体内有些区域是正常态的细棒(或平板)形式，每个正常区都被超导区所包围，这种混合态即被称之为涡旋态。在涡旋态当中，外磁场将均匀地穿透薄的正常区，而且磁场也将或多或少传进周围的超导材料当中。

第一类超导体与第二类超导体的对比第一类和第二类超导体的超导电性机制没有差别。在零磁场中，两类超导体在超导态-正常态转变点处具有相似的热学性质。但迈斯纳效应完全不同。

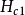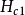好的第一类超导体完全排除磁场，直到超导电性被突然破坏，然后磁场完全穿透。好的第二类超导体完全排除磁场，直到磁场达到某 。在 以上，磁场被部分排除，但样品仍保持超导性。在更强的场 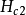下，磁通完全穿透，同时超导电性消失（样品的一个外表面层可能保持超导,直到达到某群更高的场 ）。

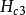第一类同第二类超导体间的一个重要差别是正常态传导电子的平均自由程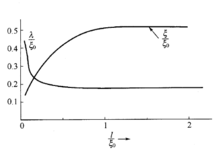的差别。如果相干长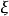度 比穿透深度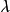 大，超导体将是第一类。大多数纯金属是第二类超导体，因为 。但是，如果平均自由程短，相干长度短，穿透深度大，则超导体将是第二类。

通过适量地掺人一种合金元素，能够把某某些金属从第一类变为第二类。在铅中加入2%（质量）的钢，能使铅从第一类变为第二类，虽然转变温度几乎一点也不变。这种掺杂性的合金化对铅的电子结构没有本质影响，但在超导态下的磁性行为发生剧烈变化。

第二类超导体的理论是Ginzburg、Laudau、Abrikosov和Gorkov提出来的，后来Kunzler及其合作者观测到Nb3Sn线在接近100kG的磁场下能负载大的超导电流，这推动了强场超导磁体的商业化开发。

考虑一个超导区域与一个正常区域之间的界面，界面具有表面能，可以是正的或者是负的，而且随外磁场的增强而减小。如果表面能总是正的，则超体是第一类；如果当磁场增加表面能变负，则是第二类超导体。表面能的正负对于转变温度没有重要影响。

涡旋态的由来当磁场被排出，块体超导体的自由能增加，但是纵向（平行于膜的方向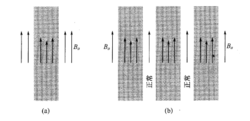）的磁场能几乎均匀地穿透很薄的膜，只有一部分磁通被排出。同时，随着外磁场的增强，超导膜的能量仅缓慢地增加。这就使破坏超导电性所需的磁场强度大为提高。膜具有通常的能隙，并且将是无电阻的。薄膜不是第二类超导体,但关于膜的研究结果表明：在适当的条件下超导电性能够在高磁场下存在。

关于薄膜结果提出这样一个问题：是否存在超导体在磁场中的稳定结构，其体内有些区域是正常态的细棒(或平板)形式，每个正常区都被超导区所包围？在这种被称之为涡旋态的混合态中，外磁场将均匀地穿透薄的正常区，而且磁场也将或多或少传进周围的超导材料当中。

涡旋态一词描述贯穿整个块体样品的涡旋形式的超异电流环流。在涡旋态下，正常区同超导区之间没有化学上的或晶体学上的差别。因为外场穿透进入超导材料，使表面能变为负，所以涡旋态是稳定的。在一定的磁场范围内即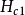 和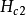 之间，保持稳定的涡旋态是第二类超导体的特征。

形成涡旋态的条件随着外加磁场的增强，形成涡旋态的起始条件是什么呢？根据穿透深度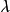 ，我们可以估算 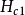。如果外加磁场为 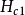，那么在包含磁通量子的正常区核中的磁场应该是 。

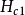从正常核向外扩展一个距离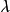 ，进入周围的超导区，这样与单个核相联系的磁通是 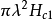，它必须等于磁通量子 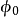。由此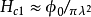（1），这是单个磁通量子的成核场。

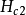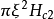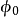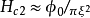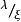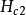在 下，磁通量子尽可能紧密地排在一起以保持超导态的条件，这意味着如相干长度所容许的那样尽可能密集。外场几乎均匀地贯穿样品，只是有微小的波动起伏，其尺度可与磁通量子晶格相比拟，每个核负载数量级为的磁通 ，后者也应量子化为 。因此（2），给出上临界场，比值 愈大，对 比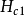 值也就会愈大。

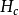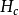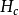我们还要寻求这些临界场与热力学临界场 之间的关系。 量度超导态的稳定能密度，该密度是 。对于第二类超导体，只能用量热法测量稳定能，以间接地确定 。为了通过 估计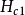 ，应该考虑在绝对零度非纯极限 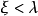下涡旋态的稳定性。这时 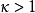，并且相干长度比穿透深度短。

我们估计在涡旋态下磁通量子核的稳定能，这核看作是负载着平均磁场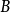 的正常金属圆柱体。半径的数量级是相干长度，即正常同超导相之间边界厚度。参照于纯超导体的能量，正常核(每单位长度)的能量由稳定能与核面积的乘积给出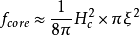：（3）。

但是由于外场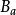 穿透到核周图的超导材料内，所以磁能降低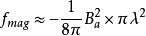：（4）。

对于单个的磁通量子，可将以上这两项相加，从而得到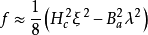：（5）。

当f