有向三面角(directed trihedral angle)指确定了方向的三面角,即规定了三条棱的一种顺序的三面角。三面角的三条棱有两种不同的循环顺序:有向三面角规定其中一种为正向,另一种为负向,从三面角的顶点向各棱所指的方向看,三条棱的两种顺序相当于顺时针或逆时针方向,两个有向三面角在三条棱的正面同为顺时针(或同为逆时针)方向时称为同向三面角,否则(即一为顺时针方向另一为逆时针方向时)称为反向三面角1。
定义依次规定三面角的棱的绕向顺序的三面角称为有向三面角。截口三角形是逆时针绕向时,称为正向三面角,否则称为负向三面角。
相关分析给定三面角S-ABC,倘若我们约定把SA,SB,SC依次叫做第一、第二、第三棱,那么便叫做有向三面角,记作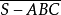 。
。

设以不通过顶点的任一平面π截三棱,从顶点S看π上的截口三角形,若围线ABCA是逆时针方向(图1左),则称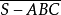 有正向;如果是顺时针方向(图1右),则称
有正向;如果是顺时针方向(图1右),则称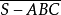 有负向,转向的正负与π的选择无关。
有负向,转向的正负与π的选择无关。
倘若反向延长三面角S-ABC的三棱,得一新三面角S-A'B'C'(图2),称为S-ABC的对顶三面角。若将SA与SA',SB与SB',SC与SC'相对应,那么显见两个三面角S-ABC和S-A'B'C'的对应的面角相等,对应的二面角相等;但它们的转向相反。
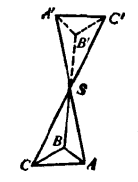
两个对顶三面角虽有对应相等的面角和二面角,在一般情况下却是无法叠合的。因在一般情况下,S-ABC的三个面角不相等,所以S-A'B'C'中只有B'SC'面能和BSC面相叠合,因此,倘若两个三面角能叠合,只有棱SA和SA'相叠合;同理SB须与SB'叠合,SC与SC'叠合,但这是不可能的:当SB’、SC'分别与SB、SC叠合以后,由于这两个三面角有反向,棱SA且和SA'各在平面BSC的一侧,决不可能叠合。
有向三面角的性质有向三面角有以下性质:
(a)若互换三面角的两棱,就改变了它的转向,即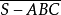 和
和 的向相反。
的向相反。
(b)若轮换三面角的三棱,它的向保持不变。即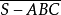 和
和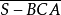 及
及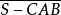 的向相同。
的向相同。
(c)假若三面角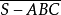 的前两棱SA,SB分别重合于三面角
的前两棱SA,SB分别重合于三面角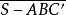 的相应两棱,则两个三面角同属于一类(有同一之向)或分属于两类(有相反之向),要看两棱SC,SC'在平面ASB的同侧或异侧而定2。
的相应两棱,则两个三面角同属于一类(有同一之向)或分属于两类(有相反之向),要看两棱SC,SC'在平面ASB的同侧或异侧而定2。
(d)两三面角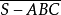 ,
,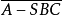 不属于同类(有相反之向)。
不属于同类(有相反之向)。
空间所有三面角的集,可以分作两类具有性质(a)—(d),而且只有一种分法。
本词条内容贡献者为:
何星 - 副教授 - 上海交通大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

