弗罗贝尼乌斯不等式(Frobenius inequality)亦称西尔维斯特不等式,是一种特殊不等式,指矩阵乘积的秩与其因子的秩之间的重要关系式。设矩阵A和B是可乘的,而B和C是可乘的,则r(ABC)≥r(AB)+r(BC)-r(B),在此不等式中,若A为m×n矩阵,B为n阶单位矩阵,C为n×s矩阵,则r(AC)≥r(A)+r(C)-n,有的书籍也称第一种情况为弗罗贝尼乌斯不等式,第二种情况为西尔维斯特不等式1。
基本介绍设A、B、C分别为m×n,n×s,s×t矩阵,则:r(ABC)≥r(AB)+r(BC)-r(B)。
设 ,则r(AB)≥r(A)+r(B)-n2。
,则r(AB)≥r(A)+r(B)-n2。
弗罗贝尼乌斯不等式的证明弗罗贝纽斯(Frobenius)不等式
设A、B、C分别为m×n,n×s,s×t矩阵,则:r(ABC)≥r(AB)+r(BC)-r(B)。
证明: 只要证明:
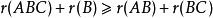 即可。
即可。
事实上,因为
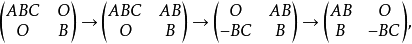 所以
所以
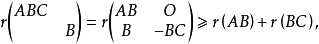 即
即

下面西尔维斯特(Sylvester)不等式也可由弗罗贝纽斯不等式的直接推得。故有的书籍也将其称为弗罗贝纽斯不等式。
西尔维斯特(Sylvester)不等式
设 ,则r(AB)≥r(A)+r(B)-n。
,则r(AB)≥r(A)+r(B)-n。
证明 只要证明:
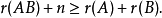 事实上,由
事实上,由
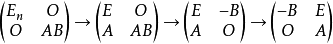 知
知
 证完2。
证完2。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

