径割是平面几何术语,指两圆的一种特殊位置关系。若一个圆通过另一个圆的一条直径的两个端点,则称这个圆径割另一个圆。
简介径割是平面几何术语,指两圆的一种特殊位置关系。若一个圆通过另一个圆的一条直径的两个端点,则称这个圆径割另一个圆。
图示如图,已知AB为⊙O1的直径,⊙O2通过A,B两点,则称⊙O2径割⊙O1。也就是说两圆的公割线为其中一圆的直径。
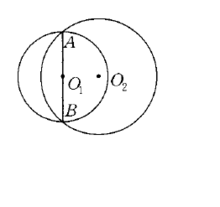
公割线(common secant)
公割线是与两圆相交的直线。两圆相交,过两交点的直线称为两圆的公割线。
公割线上两交点间的弦称为两圆的公共弦,连心线垂直于两圆的公割线,并垂直平分公共弦。1
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

