复二次型是一类重要的二次型，指复数域上的二次型，任意复二次型f(x1，x2，…，xn)都可经复满秩线性代换化为形如y²1+y²2+…+y²r的标准形，其中r是二次型f的秩。这种标准形是由f所惟一确定的，称为复二次型f的规范型，亦称正规型。两个n元复二次型等价的充分必要条件是：它们有相同的秩1。

复二次型是一类特殊的二次型，复数域C上的二次型，称为复二次型，任一复二次型φ(x1，x2，…，xn)必与一复规范形的二次型y²1+y²2+…+y²r等价。这里r是此二次型的秩，两个复二次型当且仅当它们的秩相同时等价2。

给定一个n元复二次型，可以用一个适当的非退化线性替换，把二次型化成标准形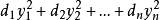，当原二次型的秩为r(r>0)时，标准形中非零平方项的个数为r，不妨设它的前r个平方项是非零的，那么上述标准形可以写成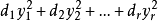，已知二次型的 标准形不唯一，那么能不能在标准形巾找到一个典型代表，使得它具有特别简单的形式？注意到每一个非零复数有两个平方根，因此可以选取di的一个平方根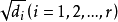，并作右边的线性替换，显然这个线性替换是非退化的，它把上述标准形变成

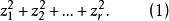由于二次型的等价关系具有传递性，上式也是原二次型的一个标准型，其形式无疑是最简单的，又由于标准形(1)中非零平方项的个数等于原二次型的秩，而秩是一个不变量，因此标准形(1)是唯—的，称为原二次型的复规范形，简称为规范形。当二次型的秩为零时，补充规定，它的规范形为0，这就得到

定理1 每一个秩为r(r>0)的n元复二次型都可以经过一个适当的非退化线性替换化成复规范形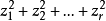，并且复规范形是唯一的3。

由于二次型的等价关系具有对称性和传递性，由上述定理立即得到：

推论2 两个n元复二次型是等价的当且仅当它们有相同的复规范形，或者当且仅当它们有相同的秩。

用矩阵的语言，定理1和推论2可以叙述如下：

定理3 秩为r(r>0)的n阶复对称矩阵A必合同于Jr，这里Jr是A的相抵标准形，即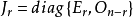，称为A的复规范形，简称为规范形。

推论4 两个n阶复对称矩阵是合同的当且仪当它们有相同的复规范形，或者当且仅当它们有相同的秩。

全体n元复二次型按照二次型的等价关系进行分类，一共可以分成n+1类，所有秩为r的n元复二次型恰好构成其中的一个类，因而可以选取复规范形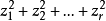作为这类二次型的代表。

上述结论可以用矩阵的语言叙述如下：全体n阶复对称矩阵按照矩阵的合同关系进行分类，一共可以分成n+1类，所有秩为r的n阶复对称矩阵恰好构成其中的一个类，因而可以选取复规范形Jr作为这类矩阵的代表3。

本词条内容贡献者为: