麦克劳林三等分角线(Maclaurin trisectrix)又名马克劳林三等分角线，是在笛卡尔直角坐标中方程式x³+xy²+ay²-3ax²=0的平面曲线(抛物线的垂足曲线)，是史路士蚌线的特殊情况(若那里k²=4a²)。

基本介绍麦克劳林三等分角线是可用于将一角三等分的平面曲线，从抛物线的焦点F关于准线的对称点O，引此抛物线的切线的垂线，垂足的轨迹叫做麦克劳林三等分角线。设OF=4a，抛物线的方程为y=4a(x-3a)，则麦克劳林三等分角线的方程为x(x²+y²)+a(y²-3x²)=0。

若取点B(2a，0)为极点，BF为极轴，则方程可化为ρ cos(θ/3)=a，在麦克劳林三等分角线上任取点M(ρ，θ)作以极半径ρ为斜边，定长a为直角边的直角三角形ABC，则∠ABC=θ/3，因而可用于将角θ三等分1。

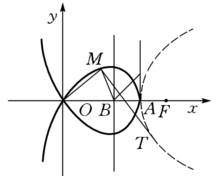
三等分角线解释：（1）三等分角线是由x³+xy²+ay²-3ax²=0确定的平面曲线，可用来解决三等分角问题。它是由马克劳林(C.Maclaurin，苏格兰，1698—1746)提出的。、

（2）三等分角线是一种特殊曲线，指可用于将角三等分的曲线。例如，蚌线、阿基米德螺线等都是三等分角线。

三等分角问题三等分角问题是希腊三大几何作图问题之一，即仅用直尺与圆规是否可以三等分任意角。限定直尺只能过一点或两点画直线，圆规只能在已知圆心、半径时画圆。

1837年，法国数学家旺策尔(P.-L.Wantzel)证明了可尺规作图的量必须满足一个2次的方程，进而推出：在一般情况下，尺规三等分任一角是不可能的.这里的结论是有一定限制的，限定“一般情况下”，因为存在无穷多个角是可以尺规三等分的.例如，可以证明：当m，n是互素的正整数，且n不能被3整除时，角

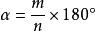或

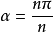是可以尺规三等分的.显然，这样的α有无穷多2。

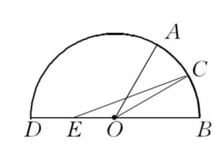
尺规作图三等分任一角，只能得到近似值.近似三等分任意角的尺规作图中，精度较高且作图简单的当属拉姆(J.F.Lamb)在1988年给出的作图(见图1).设∠AOB为已知角，以O为圆心画圆弧交两边于A，B，BO的延长线交圆于D.作∠AOB的平分线OC，取OD的中点E，连结EC，则

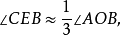
经计算，当∠AOB≤90°时，

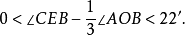如果不限定尺规作图，则最简单的三等分角的方法是古希腊数学家阿基米德(Archimedes)给出的，如图2所示.在直尺边缘上添加一点P，命尺端为O.设所要三等分的角是∠ACB，以C为圆心，OP为半径作半圆交角边于A，B.使点O在AC延长线上移动，使点P落在圆周上且使尺通过点B，连结OB.由于OP=PC=CB，则

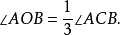德国数学家比伯巴赫(L.Bieberbach)证明了：如果使用直角尺和圆规，则可以三等分任一角.1982年，邓肯(E.B.Dynkin)和巴尼厄(W.Barnier)证明了：在一般情况下，尺规作图p等分任意角是不可能的，其中p为奇素数2.

几何三大“难题”

几何三大“难题”是古希腊人提出的三个(初等)几何学的著名“难题”：三等分角问题、倍立方问题及化圆为方问题。即要求用圆规与直尺分别实现：

(1)三等分一个任意角;

(2)作一个立方体，使它的体积等于已知立方体的两倍;

(3)作一正方形，使它的面积等于已知圆的面积。

1837年万策尔给出了前两个问题不可能性的证明;

1882年，林德曼证明了π为超越数，由此得出化圆为方问题的不可能性。因此，这三个问题是不可能问题，而不是难题。数学爱好者不要为此耗费精力。

如果取消只用尺规作图的限制，例如利用刻度尺、量角器或某些曲线(如三等分角线、割圆曲线等)，就可以解决这些问题。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学