McKay对应 (McKay correspondence)，是一种连结几何、组合学和代数的基本关系。基本关系解释了几何原本结尾的柏拉图立体分类。

简介McKay对应(McKay correspondence)，是一种连结几何、组合学和代数的基本关系。基本关系解释了几何原本结尾的柏拉图立体分类。1

代数方面设

SU(2)是两维的幺正群；

R系SU(2) 的基本（两维）表示；

G 系 SU(2) 的有限子群；

{R[i] | i∊ I }是G的全部唔约得表示；

m[i,j] 是整数，描述张量积分解：R[i] ⊗R = m[i,j] R[j]；

再设 Γ 是幅有向图，其顶点相应各 i∊ I ，再由顶点 i 向顶点 j 画 m[i,j]支箭嘴。

只有，McKay 指：

这幅图是A、D 或 E 型的仿射Dynkin图。1

克罗内克δ函数在数学中，克罗内克函数（又称克罗内克δ函数、克罗内克δ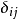）是一个二元函数，得名于德国数学家利奥波德·克罗内克。克罗内克函数的自变量（输入值）一般是两个整数，如果两者相等，则其输出值为1，否则为0。

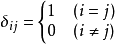
克罗内克函数的值一般简写为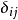。克罗内克函数和狄拉克δ函数都使用δ作为符号，但是克罗内克δ用的时候带两个下标，而狄拉克δ函数则只有一个变量。1

李代数数学上，李代数是一个代数结构，主要用于研究象李群和微分流形之类的几何对象。李代数因研究无穷小变换的概念而引入。“李代数”（以索菲斯·李命名）一词是由赫尔曼·外尔在1930年代引入的。在旧文献中，无穷小群指的就是李代数。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学