在数学中，梅林变换是一种以幂函数为核的积分变换。1

定义定义式如下：

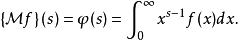
而其逆变换为

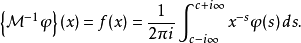梅林变换有许多应用，例如可以证明黎曼ζ函数的函数方程。2

与其他变换之关系双边拉普拉斯变换双边拉普拉斯变换可以用梅林变换1来表示，如下式

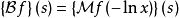梅林变换也可以用双边拉普拉斯变换来表示，如下式

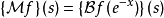
傅立叶变换傅立叶变换可以用梅林变换来表示，如下式

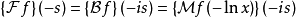梅林变换变换也可以用傅立叶来表示，如下式

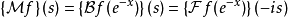
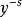范例Cahen–Mellin 积分对于 ，且 在主要分支（principal branch）上，我们有

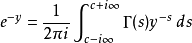其中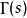 为 Γ函数。

数论假设

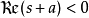我们有

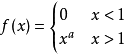其中

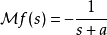
圆柱坐标系下的拉普拉斯算子在任何维度的圆柱坐标系中，拉普拉斯算子总是会包含下式3

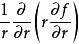
例如，拉普拉斯算子在二维空间的极坐标表示法

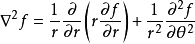或是在三维空间的柱坐标表示法

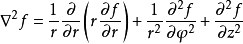而利用梅林变换可以很简单的处理此项

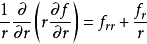
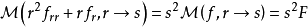
举例来说，二维拉普拉斯方程的极坐标表示法具有以下形式

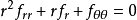或是

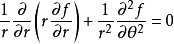
利用梅林变换，可以转换成一个简谐振子的形式

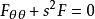
通解为：

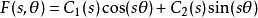
给定边界条件

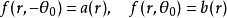
其梅林变换为

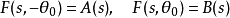则通解可以写成

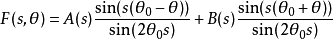最后利用逆变换以及卷积定理

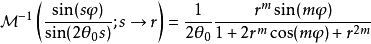其中

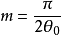可以得到

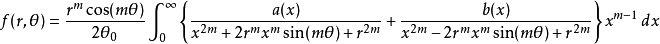
本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学