有补格(complemented lattice)亦称有余格，是一种特殊的有界格，在有界格〈L，≤〉中，对于L中的任意元素a，如果存在b∈L，使得a+b=1，a·b=0，则称元素b是元素a的补元。如果一个有界格的每个元素都至少存在一个补元，则此格称为有补格。补元是对称的，如果a是b的补元，则b也是a的补元，也可以说，a和b这两个元素是互补的，对于任一元素a∈A，可以存在多个补元，也可以不存在补元1。

基本介绍设是有界格,a,b是L中的两个元，若a∨b=1,a∧b=0，则称a是b的补元或b是a的补元，或称a和b互为补元2。

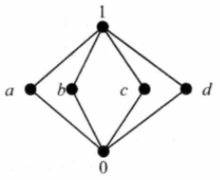
一般地说，有界格中的元素不一定有补元，一个元素有补元也不必是唯一的。例如图1所示的格中，a没有补元，b有两个补元，它们是d和c。

在图2所示的格中，每个元素有且仅有一个补元，其中a和a'，b和b'，c和c'，0和1是四对互补的元素。

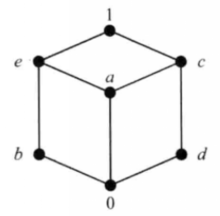
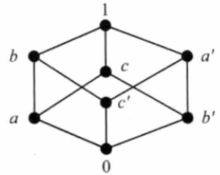
显然，在有界格中，0是1的唯一补元，1是0的唯一补元。

有补格在一个有界格中，如果每个元素都至少有一个补元，则称此格为有补格(Complemented Lattice)。对于任一元素a∈A，可以存在多个补元，也可以不存在补元。例如，在上图所示的有界格中，因为d∨c=1和d∧c=0，所以d和c是互补的，但b没有补元，而a和d都是e的补元2。

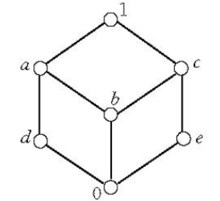
【例1】图4所示的格是有补格，其中a和b，a和d, c和b, c和d是四对互补的元素，图5所示的格也是有补格，其中a，b，c, d四个元素中任意两个都是互补元2。

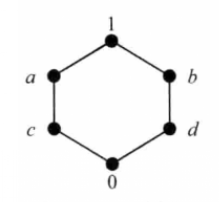
相关定理定理1设是有界格且是分配格，a∈L，若a在L中有补元，则必是唯一的。

证明若b和c都是a在L中的补元，则有avb=1，a∧b=0，a∨c=1,a∧c= 0。

由于b=c，所以a的补元唯一。

因此,有补分配格中毎一个元素有且只有一个补元，于是，若是有补分配格，是它透导的代数系统,则可在L中定义一种“补”的一元送算"－",对L中的任意一个元素a,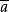 表示a的补元，这样由有补分配格秀导的代数系统也记为或,其中0, 1分别是最小元和最大元。

定理2 设是有补分配格诱导的代数系统,则对a,b∈L有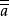 =a,

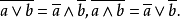
证明 由补元的定义可知, a和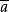 是互补的,就是说 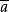的补元是a，所以 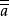=a,由

(a∨b)∨(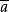∧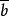)=((a∨b)∨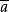)∧((a∨b)∨)

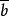= (b∨(a∨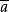))∧(a∨(b∨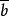)=(b∨1)∧(a∨1)=1∧1= 1

和

(a∨b)∧(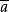 ∧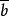)=(a∧( 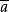∧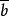))∨(b∧( 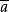∧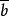))=((a∧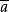)∧)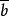∨((b∧)∧)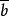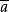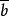

= (0∧ )∨(0∧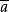)=0∨0=0

可知a∨b的补元位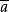∧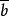,因为有补分配格中任一元素的补元是唯一的, 所以 。

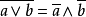同理可证。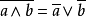

定义 有补分配格称为布尔格2。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学